Least Square Linear Regression with P Norm Regularization Where $ 1 \leq P \leq 2 $

Question

I'm taking a ML course , recently we were given an assignment , where we were asked to implement a Least Squared Linear Regression with Regularization with P-norm where $1\leq\,P\leq2$ , $p=1$ for lasso and $p=2$ for ridge , now we are asked to implement a generalized solution so it can solve for any value between $1$ and $2$ , Is that really possible ? Currently I'm able to solve the ridge case using gradient descent with Constant step size . But am not getting how to approach the solution if it needs to be solved for any value of $P$ between $1$ and $2$.

The Objective Function:

$$ \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{p} $$

Where $ 1 \leq p \leq 2 $ is given.

Answer 1

There are 2 similar problems:

Problem I

$$ \arg \min_{x} \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{p} $$

Problem II

$$ \arg \min_{x} \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{p}^{p} $$

Solution Problem I

The function is given by:

$$ f \left( x \right) = \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{p} $$

The derivative is given by:

$$ \frac{d}{d x} f \left( x \right) = {A}^{T} \left( A x - b \right) + \lambda p X x $$

Where the matrix $ X $ is a diagonal matrix given by:

$$ {X}_{ii} = \left| {x}_{i} \right|^{p - 2} \frac{\left\| x \right\|_{p}^{ \frac{1}{p} - 1 }}{p} $$

The derivative vanishes at:

$$ x = \left( {A}^{T} A + \lambda p X \right)^{-1} {A}^{T} b $$

Since $ X $ dpends on $ x $ the method to solve it is using the Iterative Reweighted Least Squares (IRLS):

$$ {x}^{k + 1} = \left( {A}^{T} A + \lambda p {X}^{k} \right)^{-1} {A}^{T} b $$

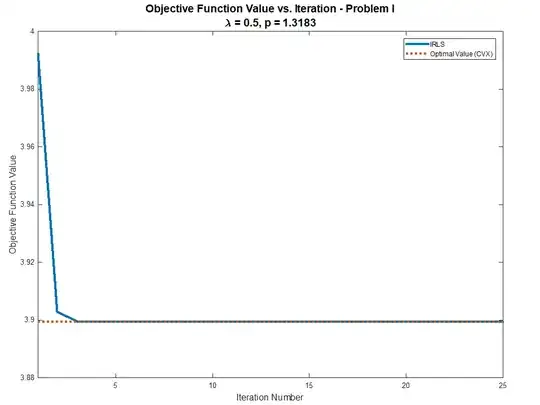
The Code:

%% Solution by Iterative Reweighted Least Squares (IRLS) - Problem I

hObjFun = @(vX) (0.5 * sum((mA * vX - vB) .^ 2)) + (paramLambda * norm(vX, paramP));
vObjVal = zeros([numIterations, 1]);

mAA = mA.' * mA;
vAb = mA.' * vB;

vX          = mA \ vB; %<! Initialization by the Least Squares Solution
vObjVal(1)  = hObjFun(vX);

for ii = 2:numIterations

    mX = diag((sum(abs(vX) .^ paramP) .^ ((1 / paramP) - 1)) .* abs(vX) .^ (paramP - 2));

    vX = (mAA + (paramLambda * mX)) \ vAb;

    vObjVal(ii) = hObjFun(vX);
end

Solution Problem II

The function is given by:

$$ f \left( x \right) = \frac{1}{2} \left\| A x - b \right\|_{2}^{2} + \lambda \left\| x \right\|_{p}^{p} $$

The derivative is given by:

$$ \frac{d}{d x} f \left( x \right) = {A}^{T} \left( A x - b \right) + \lambda p X x $$

Where the matrix $ X $ is a diagonal matrix given by:

$$ {X}_{ii} = \left| {x}_{i} \right|^{p - 2} $$

The derivative vanishes at:

$$ x = \left( {A}^{T} A + \lambda p X \right)^{-1} {A}^{T} b $$

Since $ X $ dpends on $ x $ the method to solve it is using the Iterative Reweighted Least Squares (IRLS):

$$ {x}^{k + 1} = \left( {A}^{T} A + \lambda p {X}^{k} \right)^{-1} {A}^{T} b $$

Where:

$$ {X}_{ii}^{k} = \left| {x}_{i}^{k} \right|^{p - 2} $$

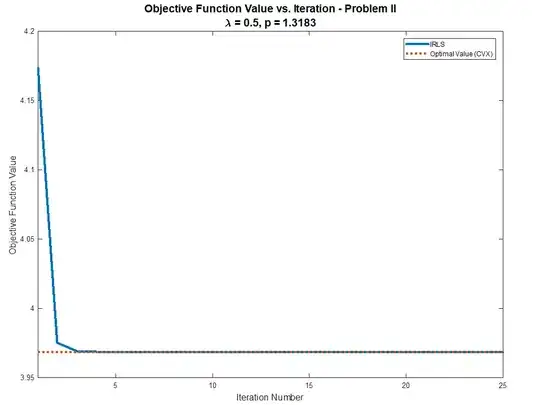
The Code is given by:

%% Solution by Iterative Reweighted Least Squares (IRLS)

hObjFun = @(vX) (0.5 * sum((mA * vX - vB) .^ 2)) + (paramLambda * sum(abs(vX) .^ paramP));
vObjVal = zeros([numIterations, 1]);

mAA = mA.' * mA;
vAb = mA.' * vB;

vX          = mA \ vB; %<! Initialization by the Least Squares Solution
vObjVal(1)  = hObjFun(vX);

for ii = 2:numIterations

    mX = diag(abs(vX) .^ (paramP - 2));

    vX = (mAA + (paramLambda * paramP * mX)) \ vAb;

    vObjVal(ii) = hObjFun(vX);
end

The code is available (Including validation by CVX) at my StackExchange Mathematics Q2403596 GitHub Repository.

Answer 2

There are many ways of optimizing functions of this form. In the case that you have $1< p < \infty$ note that your function is differentiable, so you can use some simple stochastic gradient descent method (this can also be done in the $p=1$ case, but it gets a bit hairy, though it often will converge nicely).

Additionally, I would recommend (for the step size in gradient descent) to use a decreasing step size that is not summable, e.g. you want $\alpha_k \to 0$ but $\sum_k \alpha_k = \infty$ (for example, $\alpha_k = \alpha_0/k$) since this will speed up convergence and be less sensitive to hyperparameters.

If you're really excited about using the notion that it is convex, you can use a proximal gradient approach which will work for all values of $1\le p \le \infty$ : Boyd '13 is a nice reference though you'll have to work out some of the duals of these functions (these should be quite straightforward, but it may be some extra work).

A Newton method approach will actually do quite well here, too, so long as your regularization parameter isn't too large.