1

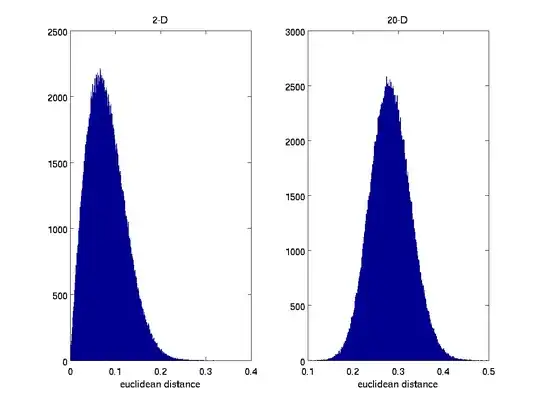
Suppose that I have a random vector $Z = [Z_1,\dots,Z_d]$ where $Z_d \sim \text{beta}(30,30)$ i.i.d. We know that the pdf of this random vector is maximized at $[0.5,\dots,0.5]$. Consider 2 cases, when $d=2$ and $d=20$. I generated samples of $Z$ using Matlab. Using these samples, I computed the euclidean norm of each from $[0.5,\dots,0.5]$ and plotted the histogram of the euclidean norm below, for $d=2$, left, and $d=20$, right.

It is expected that the ranges on the x-axis are different and that the euclidean norms for the 20-D case are larger. But why is the skewness different? The histogram for the 2-D case is more skewed to the right which means that more of its samples are closer to $[0.5,0.5]$. However, the same cannot be said for the 20-D case. It appears that there are fewer samples closer to $[0.5,\dots,0.5]$ than are farther from it which is strange as the pdf is maximum at $[0.5,0.5,\dots,0.5]$...

Can anyone explain how to make sense of this?

enter image description here

Tomas Jorovic
  • 3,983
  • 3
  • 27
  • 38
  • 1
    I think so. PDFs can be thought of as glorified histograms, so if a lot of the mass is centered somewhere, much of the data lies there. – Sean Roberson Aug 22 '17 at 21:27

1 Answers1

1

The different skewness is largely because Euclidean distances are nonnegative, meaning that while in high dimensions there is a close normal approximation, in low dimensions that is not possible.

Your 20D version could take values between $0$ and $\sqrt{5}\approx 2.2$, but has a mean of about $0.283$ and a standard deviation of about $0.044$ and is almost normally distributed with minimal skewness, and would get closer to being normally distributed at even higher dimensions. Virtually no values are very close to $0$, as your histograms show.

The lack of points close to $0$ in the 20D case should not be a surprise: it only takes one of the $20$ random variables to have a substantially non-zero value to ensure the distance is substantial and this is more likely in higher dimensions: in machine learning this is the curse of dimensionality

Your 2D version could take values between $0$ and $\sqrt{\frac12}\approx 0.7$, but has a mean of about $0.08$ and a standard deviation of about $0.041$. It cannot be close to normally distributed as the density must fall to zero at $0$, which is within two standard deviations of the mean; the upper bound is much looser so the right tail is heaver, leading to right skewness of the distribution

There is more to it than that, such as your starting Beta distribution and the square-root employed in calculating the distance (see an earlier question also looking at the distributions of random distances in different dimensions), but this is the key point

Henry
  • 157,058
  • Thanks for the reply, Henry. I used 500,000 samples to generate the 2 histograms above. Do you think that with more samples for the 20-D case, the proportion of samples closer to zero will be larger? (of course, due to memory issues I cannot generate so many samples for the 20-D problem). – Tomas Jorovic Aug 23 '17 at 00:34
  • I think $500,000$ iterations are enough to establish an accurate impression. More iterations might yield a histogram that is smoother, but not one with a fundamentally different shape. // You might consider using kernel density estimators as better approximations to density functions. – BruceET Aug 23 '17 at 01:24