Find the area of the triangle defined in the figure provided

Question

Find the area of the triangle defined in the figure below

This question appeared in a math olympiad contest and was considered invalid later on without any specific reason. Is it solvable? If yes, provide the answer!

Answer 1

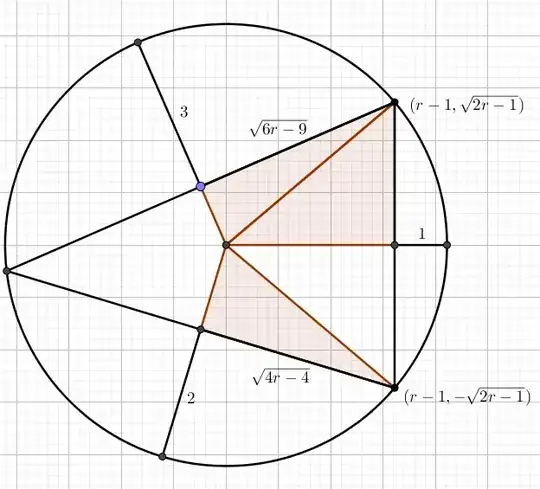
In $\triangle ABC$, $|BC|=a$, $|CA|=b$, $|AB|=c$, points $D,E,F$ are midpoints, $|D_1D_2|=|E_1E_2|=|F_1F_2|=2\,R$.

Using the power of a points $D,E$ and $F$ with respect to the circumscribed circle with radius $R$, we have

\begin{align} \tfrac{a}2\cdot\tfrac{a}2&=2\cdot(2\,R-2) ,\\ \tfrac{b}2\cdot\tfrac{b}2&=1\cdot(2\,R-1) ,\\ \tfrac{c}2\cdot\tfrac{c}2&=3\cdot(2\,R-3) ,\\ a&=4\sqrt{R-1} ,\\ b&=2\sqrt{2\,R-1} ,\\ c&=2\sqrt{6\,R-9} ,\\ S&=\frac{a\,b\,c}{4\,R} =\frac{4\sqrt3}R\,\sqrt{(R-1)(2\,R-1)(2\,R-3)}\tag{1}\label{1} ,\\ S&=\tfrac14\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} =4\sqrt{R\,(2\,R-3)}\tag{2}\label{2} . \end{align}

From $\eqref{1}=\eqref{2}$ we have \begin{align} 3\,(R-1)(2\,R-1)(2\,R-3) &= R^3 , \end{align}

and as it was noted in the comments, this results in a cubic equation

\begin{align} R^3-6\,R^2+9\,R-3&=0 \tag{3}\label{3} . \end{align}

Using substitution $R=2\,t+2$ and dividing the resulting equation by 2, we get

\begin{align} 4\,t^3-3\,t-\tfrac12&=0 . \end{align}

Using identity \begin{align} 4\,\cos^3\phi-3\,\cos\phi&=\cos3\phi \end{align}

for $\cos3\phi=\tfrac12$,

\begin{align} t&=\cos\phi =\cos\left( \tfrac13(\arccos\tfrac12+2\pi k) \right) =\cos \frac{\pi\,(1+6 k)}9 ,\quad k=0,1,2 . \end{align} Thus there are three real solutions for \eqref{3}, \begin{align} R_0&=2+2\cos\tfrac\pi9\approx 3.87938524157182 ,\\ R_1&=2+2\cos\tfrac{7\pi}9\approx 0.467911113762044 ,\\ R_2&=2+2\cos\tfrac{13\pi}9\approx 1.65270364466614 , \end{align}

and the only valid solution that satisfies condition $R>3$ is $R=2+2\cos\tfrac\pi9$, which gives the area

\begin{align} S&=4\sqrt{R\,(2\,R-3)} =4\sqrt2\sqrt{(\cos\tfrac\pi9+1)(4\,\cos\tfrac\pi9+1)} \approx 17.1865547357625 . \end{align}

Answer 2

If the circle has radius $r>3$ then the three sides of the triangle are tangent to concentric circles having radii $r-1,r-2,r-3$.

Then using just the Pythagorean relationship the lengths of the three sides of the triangle are $2\sqrt{2r-1},2\sqrt{4r-4},2\sqrt{6r-9}$.

So long as $\sqrt{2r-1}+\sqrt{4r-4}\ge\sqrt{6r-9}$ there will be a solution corresponding to $r$.

It is easily verified that solutions exist for $r=4, r=5$, whose areas will be different.