A closed form of $\sum_{n=1}^\infty\left[ H_n^2-\left(\ln n+\gamma+\frac1{2n} \right)^2\right]$

Question

The series of squares of harmonic numbers $$ \sum_{n=1}^\infty H_n^2 \tag1 $$ is divergent since $\displaystyle \lim_{n \to \infty} H_n^2 \ne 0$, actually from the classic result (6.3.18), $$ H_n=\ln n+\gamma+\frac1{2n}+O\left(\frac1{n^2}\right),\qquad \, n \to \infty, $$ where $\gamma$ is the Euler-Mascheroni constant, one gets as $n \to \infty$, $$ H_n^2=\left(\ln n+\gamma+\frac1{2n} \right)^2+O\left(\frac{\ln n}{n^2}\right)\tag2 $$which tends to infinity.

Then the following new series

$$ \sum_{n=1}^\infty \color{grey}{\left[\color{#151515}{\: H_n^2-\left(\ln n+\gamma+\frac1{2n} \right)^2}\: \right]} \tag3 $$

may be seen as a sort of regularization of $(1)$. The series $(3)$ is absolutely convergent as one may directly deduce from the comparison test with a Bertrand series, using $(2)$.

Question. What is a closed form of $(3)$?

My intuition is that $(3)$ admits a closed form in terms of known constants (or here). I've used the advanced Inverse Symbolic Calculator ISC $2.0$ but it found nothing. My recent attempt, not yet fruitful, has been to convert $(3)$ into an integral representation, starting with $$ \begin{align} -\int_0^1\!\left(\!\frac1{\ln x}+\frac1{1-x}-\frac12\!\right)\!x^{n-1}\:dx&=H_n-\ln n-\gamma-\frac1{2n},\quad n\ge1, \end{align} $$ and trying to employ similar techniques used here.

Analogous considerations are here or here, one may also explore some variations of $(3)$, like $$ \sum_{n=1}^\infty \color{grey}{\left[\color{#151515}{\: H_n^q-\left(\ln n+\gamma+\frac1{2n} \right)^q}\: \right]}, \,\sum_{n=1}^\infty (-1)^n \!\color{grey}{\left[\color{#151515}{\: H_n^q-\left(\ln n+\gamma+\frac1{2n} \right)^q}\: \right]}. $$

Answer 1

Just some considerations for now.

I have proved here that $$ \sum_{n=1}^{N}H_n^2 = (N+1) H_N^2-(2N+1)H_N+2N \tag{$\color{blue}{1}$} $$ and we have: $$ \mathcal{L}^{-1}\left(\frac{\log x+\gamma}{x}\right)(s)=-\log(s)\tag{2} $$ $$ \mathcal{L}^{-1}\left(\frac{\left(\log x+\gamma\right)^2}{x}\right)(s)=-\zeta(2)+\log^2(s)\tag{3} $$ hence the partial sums of the given series can be rearranged as follows:

$$\begin{eqnarray*}\sum_{n=1}^{N}\left[H_n^2-\left(\log n+\gamma+\frac{1}{2n}\right)^2\right]&=&(\color{blue}{1})-\frac{H_N^{(2)}}{4}-\sum_{n=1}^{N}\frac{\log n+\gamma}{n}-\sum_{n=1}^{N}n\frac{(\log n+\gamma)^2}{n}\\&=&(\color{blue}{1})-\frac{H_N^{(2)}}{4}+\int_{0}^{+\infty}\frac{\log(s)(1-e^{-Ns})}{e^s-1}\,ds\\&-&\int_{0}^{+\infty}\frac{e^{-N s} \left(e^{(1+N) s}+N-e^s (1+N)\right)\left(\zeta(2)-\log^2 s\right)}{\left(-1+e^s\right)^2}\,ds\end{eqnarray*}$$

If we find a way to distribute $(\color{blue}{1})$ over the last two integrals, in a way ensuring they are convergent integrals as $N\to +\infty$, we are done. At first sight the closed form of the LHS appears to be related with $\zeta(2)$, $\zeta'(0)=-\frac{1}{2}\log(2\pi)$ and $$ \zeta''(0)=\frac{\gamma^2}{2}-\frac{\pi ^2}{24}-\frac{1}{2}\log^2(2\pi)+\gamma_1$$ with $\gamma_1$ being a Stieltjes constant. An alternative, brute-force way is just to compute the asymptotic expansions of $$ \sum_{n=1}^{N}\log^2(n),\qquad \sum_{n=1}^{N}\frac{\log(n)}{n} $$ with the sufficient degree of accuracy (I guess that to stop at the $O\left(\frac{1}{N^3}\right)$ term is enough), that is just a tedious exercise about summation by parts.

Answer 2

The given series admits a closed form.

Proposition.$$ \sum_{n=1}^\infty \color{grey}{\left[\color{#151515}{\: H_n^2-\left(\ln n+\gamma+\frac1{2n} \right)^2}\: \right]}=\frac12\ln^2(2\pi)-\gamma\ln (2\pi)-\frac12\gamma^2-2\gamma_1-1. \qquad (\star) $$

where $\gamma_1$ is a Stieltjes constant.

(Sketch of a proof).

Let us consider, for $a\ge 0$, $$ S(a):=\sum_{n=1}^\infty \color{grey}{\left[\color{#151515}{\: \left(\psi(n+a+1)+\gamma\right)^2-\left(\ln (n+a)+\gamma+\frac1{2(n+a)} \right)^2}\: \right]}, \tag1 $$ where throughout $\displaystyle \psi :=\left(\text{Log}\: \Gamma \right)'$ is the digamma function. From the standard identity $$ \psi(n+1)+\gamma=H_n\qquad n=1,2,\cdots,\tag2 $$ we have $$ S(0)=\sum_{n=1}^\infty \color{grey}{\left[\color{#151515}{\: H_n^2-\left(\ln n+\gamma+\frac1{2n} \right)^2}\: \right]}. \tag3 $$ One is allowed to differentiate $S(a)$ termwise obtaining $$ \begin{align} S'(a)=\sum_{n=1}^\infty &\left[2\:\psi'(n+a+1)\left(\psi(n+a+1)+\gamma\right)\color{#FFFFFF}{\frac2{(n+a)}}\right. \\&-\left.\left(\frac2{(n+a)}-\frac1{(n+a)^2}\right)\!\left(\ln (n+a)+\gamma+\frac1{2(n+a)} \right)\right], \tag4 \end{align} $$ then we are lead to consider the partial sum, $$ \begin{align} S_N'(a)=&\sum_{n=1}^N 2\:\psi'(n+a+1)\left(\psi(n+a+1)+\gamma\right) \\-&\sum_{n=1}^N\left(\frac2{(n+a)}-\frac1{(n+a)^2}\right)\left(\ln (n+a)+\gamma+\frac1{2(n+a)} \right).\tag5 \end{align} $$ We have proved here that $\displaystyle \sum_{n=1}^N \psi'(n)\psi(n)$ has a closed form, this result can be extended as follows.

Theorem. Let $a$ be any non-negative real number. We have $$ \begin{align} &\sum_{n=1}^N \psi'(n+a+1)\psi(n+a+1) \\&=\left((N+a+1) \psi(N+a+2)-(a+1)\psi(a+2)\right)' \psi(N+a+1) \\\\&-\left((N+a+1) \psi(N+a+2)-(a+2)\psi(a+3)\right)' \\\\&+\left((a+1)\psi(a+2)\right)'\left(\psi(N+a+1)-\psi(a+2)\right) \tag6 \\\\&+\frac12 \psi'(N+a+1)-\frac12\psi'(a+2)-\frac12 \left(\psi'(N+a+1)\right)^2+\frac12 \left(\psi'(a+2)\right)^2. \end{align} $$

Proof. One uses a summation by parts with $$ f_n(a)=\psi(n+a+1),\quad g_n(a)=\psi'(n+a+1),\quad n\ge1, $$ taking into account that $$ \begin{align} &\sum_{n=1}^N \psi'(n+a+1)=\left((N+a+1) \psi(N+a+2)-(a+1)\psi(a+2)\right)'. \tag7 \end{align} $$ Then the second sum on the right hand side of $(5)$ satisfies $$ \begin{align} &\sum_{n=1}^N\left(\frac2{(n+a)}-\frac1{(n+a)^2}\right)\left(\ln (n+a)+\gamma+\frac1{2(n+a)}\right) \\\\&=2\gamma_1(a+1)-2\gamma_1(N+a+1)+2\gamma \psi(N+a+1)-2\gamma\psi(a+1) \tag8 \\\\&+\frac14 \psi''(N+a+1)-\frac14\psi''(a+2)+\gamma_1'(a+1)-\gamma_1'(N+a+1) \\\\&+(\gamma+1)\psi'(N+a+1)-(\gamma+1)\psi'(a+1), \end{align} $$ where we have used the generalized Stieltjes constant, $$ \begin{align} \gamma_1(a+1)=\lim_{N \to \infty}\left(\sum_{n=1}^N\frac{\ln(n+a)}{n+a}-\frac12\:\ln^2 \left(N+a\right)\right). \end{align} $$ We then insert $(6)$, $(7)$ and $(8)$ into $(5)$ and let $N \to \infty$ to get

$$ \begin{align} S'(a)=&\:\left(2a-2(a+2)\psi(a+3)\right)'+\left(2\gamma a-2\gamma(a+1)\psi(a+2)\right)' \\\\-&\:\left(\psi(a+2)-(a+1) \left(\psi(a+2)\right)^2\right)'-2\gamma_1(a+1)+2\gamma\psi(a+1) \tag9 \\\\+&\frac14\psi''(a+2)-\gamma_1'(a+1)+(\gamma+1)\psi'(a+1). \end{align} $$ Finally, integrating $(9)$ using $$ 2\int_1^{1+a}\gamma_1(t)\:dt=\zeta''(0,a+1)-\zeta''(0), $$ where $\zeta(\cdot,\cdot)$ denotes the Hurwitz zeta function and where $\zeta''(0,a+1)=\left.\partial_s^2\zeta(s,a+1)\right|_{s=0}$, determining the constant of integration by letting $a \to \infty$ and using $(3)$ yields $(\star)$.

Answer 3

An integral representation for the series

Let,

$\begin{align} u_n:=H_n-\ln n-\gamma-\dfrac{1}{2n}\\ v_n:=H_n+\ln n+\gamma+\dfrac{1}{2n}\\ \end{align}$

Observe that,

$\begin{align}u_n+v_n\end{align}=2H_n$

Since,

$\displaystyle H_n=-n\int_0^1 x^{n-1}\ln(1-x)\ dx$

and,

$\displaystyle u_n=-\int_0^1 \left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)x^{n-1}\ dx$

then,

$\begin{align}v_n&=2H_n-u_n\\ &=-2n\int_0^1 x^{n-1}\ln(1-x)\ dx+\int_0^1 \left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)x^{n-1}\ dx \end{align}$

therefore,

$\begin{align}\sum_{n=1}^{\infty}u_nv_n&=\sum_{n=1}^{\infty}\left(2n\int_0^1 \int_0^1\ln(1-x)\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\right)(xy)^{n-1}\ dx\ dy-\\ &\int_0^1\int_0^1 \left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)(xy)^{n-1}\ dx\ dy\\ &=2\int_0^1\int_0^1 \frac{\ln(1-x)}{(1-xy)^2}\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dx\ dy-\\ &\int_0^1\int_0^1\frac{1}{1-xy} \left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dx\ dy\\ &=\int_0^1 \int_0^1 \left(\frac{2\ln(1-x)}{(1-xy)^2}-\frac{1}{1-xy}\left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dx\ dy\\ &=\boxed{2A-B} \end{align}$

and,

$\begin{align}A&=\int_0^1 \int_0^1 \frac{\ln(1-x)}{(1-xy)^2}\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dx\ dy\\ B&=\int_0^1 \int_0^1 \frac{1}{1-xy}\left(\frac{1}{\ln x}+\frac{1}{1-x}-\frac{1}{2}\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dx\ dy \end{align}$

( Computation of A )

( Computation of B )

Addenda:

1) $\begin{align}A=\int_0^1 \frac{\ln(1-y)}{y(1-y)}\left(\frac{1}{\ln y}+\frac{1}{1-y}-\frac{1}{2}\right)\ dy \end{align}$

(one can simplify this integral)

$A\approx -0.1932$

( Computation of A )

$\begin{align}B&=\int_0^1 \int_0^1 \frac{1}{1-xy}\left(\frac{1}{\ln x}+\frac{1}{1-x}\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-1\right)\ dx\ dy+\frac{\pi^2}{24} \end{align}$

2) Since,

$\displaystyle \gamma=\int_0^1 \left(\frac{1}{\ln x}+\frac{1}{1-x}\right)\ dx$

then

$\begin{align}B&=\int_0^1 \int_0^1 \frac{xy}{1-xy}\left(\frac{1}{\ln x}+\frac{1}{1-x}\right)\left(\frac{1}{\ln y}+\frac{1}{1-y}-1\right)\ dx\ dy+\gamma^2-\gamma+\frac{\pi^2}{24}\end{align}$

$B\approx 0.00651229$

(Computation of B )

3) $\begin{align}A&=\int_0^1\left[\left(\frac{\ln(1-x)}{x}+\frac{\ln(1-x)}{1-x}\right)\left(\frac{1}{\ln x}+\frac{1}{1-x}\right)-\frac{1}{2}\times \frac{\ln(1-x)}{1-x}\right]\ dx+\frac{\pi^2}{12}\end{align}$

( Computation of A )

Answer 4

We derive a representation of the sum in question $f$ as a double integral with a symmetric integrand. Transformation to polar coordinates leads to a explicitly "innocent" expression for the integrand in the domain of interest. It is proposed to develop the integrand into a power series. The developments are under way.

Letting

$$d(n)=\frac{1}{2 n}+\log (n)+\gamma$$

the nth summand becomes

$$s(n)=H(n)^2-d(n)^2$$

and the sum is

$$f=\sum _{n=1}^{\infty } s(n)$$

We now use the integral representations

$$d(n)\to \int_0^1 \left(x^{n-1} \left(\frac{1}{1-x}+\frac{1}{\log (x)}-\frac{1}{2}\right)+\frac{1-x^n}{1-x}\right) \, dx$$

and

$$H(n)\to \int_0^1 \frac{1-x^n}{1-x} \, dx$$

and replace the terms in the summand which then becomes a double integral (sorry for the bad Latex)

$$si(n)=\int _0^1\int _0^1\left(\frac{\left(1-x^n\right) \left(1-y^n\right)}{(1-x) (1-y)}-\left(x^{n-1} \left(\frac{1}{1-x}+\frac{1}{\log (x)}-\frac{1}{2}\right)+\frac{1-x^n}{1-x}\right) \left(y^{n-1} \left(\frac{1}{1-y}+\frac{1}{\log (y)}-\frac{1}{2}\right)+\frac{1-y^n}{1-y}\right)\right)dydx$$

The sum of $si(n)$ over $n$ can be easily done.

$$si=\sum _{n=1}^{\infty } si(n)$$

The result, called $sa1$ and is the integrand for the positive quantity $-f$ in what follows, is

$$\text{sa1}=\frac{\left(\frac{1}{1-x}+\frac{1}{\log (x)}-\frac{1}{2}\right) \left(\frac{1}{1-y}+\frac{1}{\log (y)}-\frac{1}{2}\right)+\frac{\frac{1}{1-x}+\frac{1}{\log (x)}-\frac{1}{2}}{1-x}+\frac{\frac{1}{1-y}+\frac{1}{\log (y)}-\frac{1}{2}}{1-y}}{1-x y}$$

Now we make two subsequent coordinate transformations

1. x-> Exp[-u], y->Exp[-v]
2. u->r Cos[a], v-> r Sin[a], 0<=r, 0<=a<=pi/2

This defines sa3. Instead of giving the lengthy expression we show the plot

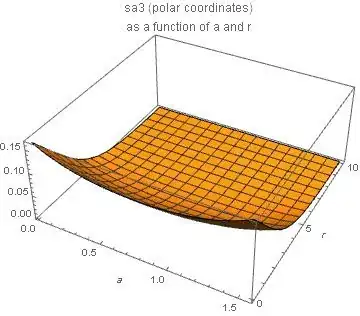
The plot shows that sa3 is a pretty innocent function.

$-f$ is now given by the integral of $sa3$ over $r$ from $0$ to $\infty$ and over $a$ from $0$ to $\pi/2$.

A numerical check gives sufficient agreement between direct sum with 10^4 terms (|sum| = 0.392733) and this integral (int =0.392733 ) to see that the integrand is correct.

Expansion of the integrand in a series of powers of $(a-\pi/4)$

I was not able to do the integral in symbolic form (neither of the two). The plot shows, however, that the dependence of the integrand on $a$ is weak so that it seems reasonable to expand the integrand in a series of (even) powers of $(a-\pi/4)$ the coefficients of which are integrals over $r$ which seem not impossible to be done in closed form.

The first term of this development (equal to $sa3$ for $a = \pi/4$) is

$$sa3(a=\pi/4)= \frac{\left(\sqrt{2} e^{\frac{r}{\sqrt{2}}} r+\sqrt{2} r-4 e^{\frac{r}{\sqrt{2}}}+4\right) \left(5 \sqrt{2} e^{\frac{r}{\sqrt{2}}} r+\sqrt{2} r-4 e^{\frac{r}{\sqrt{2}}}+4\right)}{8 \left(e^{\frac{r}{\sqrt{2}}}-1\right)^2 \left(e^{\sqrt{2} r}-1\right) r}$$

Mathematica refused to solve that integral.

Behaviour of the integrand close to the origin

The behaviour of the integrand close to the origin is not easily found in the x-y-representation, but it is easy in polar coordinates: $sa3$ close to the origin is found by expanding it into a series of powers of $r$ and doing the a-integral exactly. The first four terms are

$$ \frac{\tanh ^{-1}\left(\frac{1}{\sqrt{2}}\right)}{3 \sqrt{2}} -r \frac{\pi }{48} -r^2 \left(\frac{1}{144}-\frac{\tanh ^{-1}\left(\frac{1}{\sqrt{2}}\right)}{240 \sqrt{2}}\right)+\frac{r^3}{480}+r^4 \left(\frac{149}{181440}-\frac{\tanh ^{-1}\left(\frac{1}{\sqrt{2}}\right)}{12096 \sqrt{2}}\right)$$

Numerically,

$$0.207742 -0.0654498 r-0.00434767 r^2+0.00208333 r^3+0.000769685 r^4$$

To be continued.