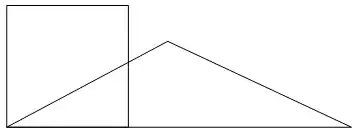
A triangle with sidelengths (3/2, 5/3, 17/6) works. The upper coordinate is at {45/34, 12/17}. Here's a picture of it with a unit square. Any heronian triangle with a square area can be used, here are two more: (3, 25, 26)/6, (17, 113, 120)/30. For more, see the Sascha Kurz heronian triangle list.
A few more: (28,1345,1371)/84, (41,357,370)/84, (104,657,697)/180, (17,4904,4905)/204, (289,2313,2600)/204, (73,1274,1299)/210, (255,353,392)/210, (40,8749,8787)/234, (305,424,567)/252, (337,441,680)/252, (130,2057,2169)/264, (520,641,1089)/330, (1009,3088,4095)/336, (113,3137,3150)/420, (245,1443,1448)/420, (800,1241,2009)/420, (56,9273,9305)/462, (539,890,1233)/462, (585,746,847)/462, (696,865,1183)/546,
(2809,4395,7202)/546, (314,2555,2619)/630, (833,1017,1066)/630, (4201,4375,8574)/630, (1000,2057,2993)/660, (377,4570,4879)/714, (544,2329,2535)/780, (1409,6596,7995)/780, (801,1825,2176)/840, (1131,1285,1904)/840, (401,4097,4290)/858, (841,1898,2307)/870,
(1617,2425,3944)/924, (1445,1476,2281)/1020, (939,2548,2785)/1092, (1241,6884,8075)/1140
