1

  1. Let $\sigma = (1, 2, 5, 4)(2,3)$ in $S_5$. Find the index of $<\sigma>$ in $S_5$

  2. Let $\mu = (1,2,4,5)(3,6)$ in $S_6$. Find the index of $<\mu>$ in $S_6$

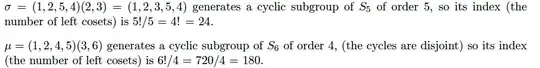
enter image description here

Here is what I don't understand.

1) This seems like an advanced method of counting. They found the number of elements in the group - the order is 5. Then they count the permutations of the big group, which is 5!. Now what I don't understand is dividing them out? I am a little lost as to why they are doing that? Could someone show me just what one coset even looks like here?

2) Same question as (1), I like to see one coset and this is just a refresher for me because I am confusing the order of a group. They say the order of the subgroup is 4 because they are disjoint because it takes 4 mappings for $\mu$ to map back to the identity, but I thought the order of a group means the number of elements. So if I were to count, isn't there still $6$ elements in $\mu$?

Lemon
  • 12,664

2 Answers2

1

If $H \subseteq G$ is a subgroup, its index $[G: H$] is the number of left cosets of $H$ in $G$. Recall that a left coset is a set $gH = \{gh : h \in H\}$ for some $g \in G$. The left cosets partition $G$ and $|gH| = |H|$ for any $g$, so if $G$ is finite $[G: H] = |G|/|H|$.

As for your second question, it looks like you need to review what the symmetric group is.
You are correct that the order of a group is the number of elements in the group. In this case $\mu$ is an element of $S_6$, and the group generated by it is

$$\{\mu, \mu^2, \mu^3, id\} = \{(1245)(36), (14)(25), (1542)(36), id \}$$

which has four elements.

Ink
  • 5,126
0

1) There are important theorems that say cosets are disjoint and have the same size. Therefore, once you believe (1,2,3,5,4) generates a subgroup of order 5, the index must be 5!/5 since the cosets partition the set of group elements into 5s.

The easiest coset to exhibit is the subgroup (call it G) itself: G={(1,2,3,5,4),(1,2,3,5,4)2,(1,2,3,5,4)3,(1,2,3,5,4)4,(1,2,3,5,4)5}={(1,2,3,5,4),(1,3,4,2,5),(1,5,2,4,3),(1,4,5,3,2),(1)(2)(3)(4)(5)}. Another left coset is (2,3)G={(2,3)(1,2,3,5,4),(2,3)(1,3,4,2,5),(2,3)(1,5,2,4,3),(2,3)(1,4,5,3,2),(2,3)(1)(2)(3)(4)(5)}={(1,3,5,4)(2),(1,2,5)(3,4),(1,5,3)(2,4),(1,4,5,2)(3),(1)(2,3)(4)(5)}

2) The order of a group is the number of elements. The things being permuted don't really relate directly. The subgroup generated by μ has four elements: {(1,2,4,5)(3,6),(1,4)(2,5)(3)(6),(1,5,4,2)(3,6),(1)(2)(3)(4)(5)(6)}. It just so happens that the four elements of that group are themselves permutations of the set (not a group) {1,2,3,4,5,6}.

Mark S.
  • 23,925
  • OKay I am very lost by example. How did you pick (2,3) from $G$? – Lemon Nov 18 '12 at 07:14
  • (2,3) is not in G. (2,3) is in $S_5$ (and I just picked it randomly), and as such, it gives rise to a left coset of G. If I had picked something in G (say, (1,3,4,2,5)) then the left coset (1,3,4,2,5) G would just be G again. It wouldn't be a new coset. – Mark S. Nov 18 '12 at 07:17
  • In response to a deleted comment, $\left((1,2,4,5)(3,6)\right)^2$ sends $3$ to $6$ and then back to $3$, so it should have $(3)$. Similarly for $(6)$. However, it sends $1$ to $2$ and then to $4$, and $4$ to $5$ and then to $1$, so it should have $(1,4)$ as part of its disjoint cycle decomposition. Similarly, it sends $2$ to $4$ and then to $5$, and $5$ to $1$ and then to $2$, so it should have $(2,5)$. – Mark S. Nov 18 '12 at 07:42
  • 1
    You don't really include single element cycles in a cycle decomposition. – Ink Nov 18 '12 at 08:14
  • So basically the answer is saying I can take 24 elements in $S_5$ like $(3,1)$, $(6,3,2)$ and multiply it to $\sigma$ and eventually that will exhaust $S_5$? – Lemon Nov 18 '12 at 08:16
  • @sizz, Not just to $\sigma$ but to $\sigma^2, \sigma^3,$ and $\sigma^4$. – Ink Nov 18 '12 at 08:25
  • @Brian re:single element cycles: It's a habit I picked up so I/my readers don't forget whether "(123)" is an element of S_5 or S_6, etc. It also avoids the confusion that might arise because I don't know whether sizz uses $\mathbf{1}$ or $e$ or $\mathrm{id}$ for identity elements. But you're right to point out it's non-standard and wasteful when there's no chance for confusion. sizz, you also need to multiply by the identity, which is also part of the subgroup generated by anything, and which coincidentally is $\sigma^5$. Also, just be careful: $(6,3,2)$ isn't part of $S_5$ – Mark S. Nov 18 '12 at 14:33
  • Actually, I could stand to be a little clearer. Since in every group (including $S_5$), elements have inverses, if you take any single element $g$ in the group, and you want to get an arbitrary element $h$, by multiplication, it's like you want to find the $k$ such that $gk=h$. But the answer to that is just $k=g^{-1}h$. So yes, you can get every element of $S_5$ just by multiplying things by $\sigma$. However, the point here is that you're not interested in getting all the elements of $S_5$ element by element, you want cosets to generate $S_5$... – Mark S. Nov 18 '12 at 14:47
  • If $G=\langle\sigma\rangle$, which has five elements, then the cosets you can get from any element of $G$ would be the same as $G$: $(1,3,4,2,5)G=G$, etc. And the coset you'd get from $(2,3)$ would be the same as the coset you'd get from $(153)(24)$ since $\left((153)(24)\right)(1,3,4,2,5)=(2,3)$. As you go through the elements of $S_5$, you generate each 5-element coset 5 separate times; there are 24 of them. Cosets never overlap: http://math.stackexchange.com/questions/99421/ and have the same size (finite grps): Thm 4.9 in http://www.math.uconn.edu/~kconrad/blurbs/grouptheory/coset.pdf – Mark S. Nov 18 '12 at 14:57