Sum of three dice is eleven

Question

the sample space of one toss of three dice is: $\Omega = \left \{ (1,1,1), ..., (6,6,6) \right \}$
so there are $6^3 = 216$ possible outcomes.

What is the probability to obtain an outcome where the sum of its three components is equal to 11?

I've considered the possible value can assume dice without a particular position and then I have considered the permutations to include every position:
$(6,4,1), 3! = 6 \\ (6,3,2), 3! = 6 \\ (5,5,1), \frac{3!}{2!} = 3 \\ (5,4,2), 3! = 6 \\ (5,3,3), \frac{3!}{2!} = 3 \\ (4,4,3), \frac{3!}{2!} = 3$

so I've summed up obtaining $27$ and the probability would be $\frac{27}{216}$

Now, consider if I have to do this same passages for sums from 3 to 18, it is very exhausting.
So, my question is: Is there any "faster" way to do that?

Answer 1

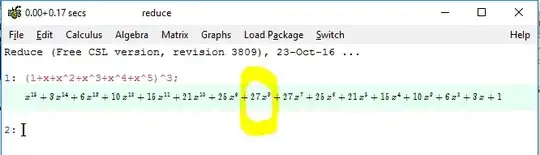
The generating function approach is to ask for the coefficients of $x^{n}$ in the expansion of:

$$(x+x^2+x^3+x^4+x^5+x^6)^{3}=x^3\left(\frac{1-x^6}{1-x}\right)^3$$

Now, $$\frac{1}{(1-x)^3}=\sum_{k=0}^{\infty}\binom{k+2}{2}x^k$$

And $$(1-x^6)^3=1-3x^6+3x^{12}-x^{18}$$

So the product of these and $x^3$ has, for the coefficient $x^n$:

$$\binom{n-1}{2}-3\binom{n-7}{2}+3\binom{n-13}{2}-\binom{n-19}{2}$$

Trick is to treat $\binom{j}{2}=0$ when $j<2.$

So, for example, when $n=11$, you get $\binom{10}{2}-3\binom{4}{2}=45-18=27$.

---

This also gives you a hint of the value when dealing with $k$ dice. Then:

$$c_n = \sum_{i=0}^{k}(-1)^i\binom{k}{i}\binom{n-(1+6i)}{k-1}$$ where in this formula, $\binom{a}{k-1}$ is zero when $a<0.$

If you don't like generating functions, this can be proven via inclusion-exclusion.

---

There's another approach that is a little faster for computing all values.

If $(1+x+x^2+\cdots+x^5)^3=a_0+a_1x+\cdots+a_nx^n+\cdots$ then you get that:

$$(a_0+a_1x+\cdots+a_nx^n+\cdots)(1-3x+3x^2-x^3)=(1-x^6)^3=1-3x^6+3x^{12}-x^{18}$$

What this means is that (setting $a_n=0$ when $n<0$: $$a_{n}-3a_{n-1}+3a_{n-2}-a_{n-3}=\begin{cases} 1&n=0\\ -3&n=6\\ 3&n=12\\ -1&n=18\\ 0&\text{otherwise} \end{cases}$$

or:

$$a_{n}=3\left(a_{n-1}-a_{n-2}\right)+a_{n-3}+\begin{cases} (-1)^k\binom{3}{k}&n=6k\\ 0&\text{otherwise} \end{cases}$$

Then the final coefficient of $x^n$, after we multiply by $x^3$ again, is $a_{n-3}$.

So you get:

$$\begin{align}a_0&=0+(-1)^{0}\binom{3}{0}=1\\ a_1&=3\left( a_0-a_{-1}\right)=3\\ a_2&=3\left( a_1 - a_0\right)=6\\ a_3&=3\left(a_2 - a_1\right)+a_0=10\\ a_4&=3\left(a_3-a_2\right)+a_1=15\\ a_5&=3\left(a_4-a_3\right)+a_2=21\\ a_6&=3\left(a_5-a_4\right)+a_3+(-1)^{1}\binom{3}{1}=25\\ &\cdots \end{align}$$

There's a special trick that can be applied here: $a_{n}=3a_{n-1}-3a_{n-2}+a_{n-3}$ is known to be a quadratic polynomial in $n$. So, when $n$ is not a multiple of $6$, you get that:

$$a_{n-2}-a_{n-3},a_{n-1}-a_{n-2},a_{n}-a_{n-1}$$ must be an arithmetic progression for any $n$ not a multiple of $6$.

So we have that $a_5-a_4 = 6, a_6-a_5=4$ and thus $a_7-a_6=2$, or $a_7=a_6+2=27.$ $a_8=27+0=27, a_9=27-2=25,a_{10}=25-4=21,a_{11}=21-6=15,a_{12}=15-8+(-1)^2\binom{3}{2}=10$.

Answer 2

For the favorable cases: Since the dice can assume integer values between $1$ and $6$, we wish to find the number of solutions in the positive integers of the equation $$x_1 + x_2 + x_3 = 11 \tag{1}$$ subject to the restrictions that $x_k \leq 6$ for $1 \leq k \le 3$.

A particular solution of equation 1 corresponds to the placement of two addition signs in the ten spaces between successive ones in a row of eleven ones. For instance, $$1 1 1 1 1 + 1 1 + 1 1 1 1$$ corresponds to the solution $x_1 = 5$, $x_2 = 2$, and $x_3 = 4$. Hence, the number of solutions of equation 1 in the positive integers is the number of ways we can select two of the ten spaces between successive ones in a row of eleven ones in which to place addition signs, which is $$\binom{10}{2}$$

More generally, the equation $$x_1 + x_2 + \cdots + x_k = n$$ has $$\binom{n - 1}{k - 1}$$ solutions in the positive integers since we must choose which $k - 1$ of the $n - 1$ spaces between successive ones in a row of $n$ ones will be filled with addition signs.

However, we have counted solutions in which one of the variables exceeds $6$. Notice that it is not possible for two of the variables to exceed $6$ simultaneously since $2 \cdot 7 = 14 > 11$.

Suppose $x_1 > 6$. Let $x_1' = x_1 - 6$. Then $x_1'$ is a positive integer. Substituting $x_1' + 6$ for $x_1$ in equation 1 yields \begin{align*} x_1' + 6 + x_2 + x_3 & = 11\\ x_1' + x_2 + x_3 & = 5 \tag{2} \end{align*} Equation 2 is an equation in the positive integers with $$\binom{5 - 1}{3 - 1} = \binom{4}{2}$$ solutions. By symmetry, there are an equal number of solutions in which $x_2 > 6$ or $x_3 > 6$. Hence, the number of solutions we must exclude is $$\binom{3}{1}\binom{4}{2}$$

Hence, the number of permissible solutions is $$\binom{10}{2} - \binom{3}{1}\binom{4}{2}$$

Addendum: You asked about the sums from $3$ to $18$. If $3 \leq n \leq 8$, then the number of solutions of the equation
$$x_1 + x_2 + x_3 = n \tag{3}$$ in the positive integers with $x_k \leq 6$ for $1 \leq k \leq 3$ is $$\binom{n - 1}{3 - 1} = \binom{n - 1}{2}$$ since it is not possible for one of the variables to exceed $6$.

Notice also that by symmetry, the number of solutions with sum $3$ (all ones) is equal to the number of solutions with sum $18$ (all sixes), the number of solutions with sum $4$ (two ones and a two) is equal to the number of solutions with sum $17$ (two fives and a six), and so forth. Hence, knowing the number of solutions for $3 \leq n \leq 8$ also tells us the number of solutions for $13 \leq n \leq 18$.

The following argument shows that the number of solutions with sum $n$ is equal to the number of solutions with sum $21 - n$. If $y_k = 7 - x_k$, then $1 \leq x_k \leq 6 \implies 1 \leq y_k \leq 6$. Moreover, substituting $7 - y_k$ for $x_k$ for $1 \leq k \leq 3$ in equation 3 yields \begin{align*} 7 - y_1 + 7 - y_2 + 7 - y_3 & = n\\ 21 - y_1 - y_2 - y_3 & = n\\ -21 + y_1 + y_2 + y_3 & = -n\\ y_1 + y_2 + y_3 & = 21 - n \end{align*}

By an argument similar to that given above for $n = 11$, the number of solutions of the equation $$x_1 + x_2 + x_3 = 9$$ in positive integers not exceeding six is $$\binom{8}{2} - \binom{3}{1}\binom{2}{2} = \binom{8}{2} - \binom{3}{1}$$ By symmetry, this is also the number of solutions for $n = 12$.

Also, by symmetry, the number of solutions for $n = 10$ is equal to the number of solutions for $n = 11$.

Answer 3

It is the coefficient of $x^{11}$ in $(x(1+x+x^2+x^3+x^4+x^5))^3$ which is indeed $\color{red}{27}$ but any which a ways you solve it will be a bit of a slog.

Answer 4

If you want a relatively efficient pencil-and-paper solution, I recommend Thomas Andrew's answer.

If you just want to avoid being exhausted by the calculations, and you are willing to use some software to help you, you can easily get the probabilities with the help of a spreadsheet. Rather than replicate answers to other questions, let me just refer you to this answer, in which I gave a spreadsheet for twenty-sided dice, and this answer, in which I adapted the spreadsheet to work for six-sided dice.

Of course if you really just want a quick answer you can ask Wolfram Alpha. The spreadsheet, however, has the slight advantage (in my opinion) that you can examine it to see how the probabilities are derived.

Answer 5

Noodling out.

If the first die is $a $ then we need that the second die and the third die add to $11-a$ which means the second die is between $\max (1,11-a-6)=\max (1,5-a) $ and $\min (6,11-a-1)=\min (6,10-a) $.

So the probability is $\sum\limits_{a=1}^6\sum\limits _{b=\max (1,5-a)}^{\min (6,10-a)}\frac 16*\frac 16*\frac 16$

$=\frac 1 {216}\sum_{a=1}^6 \min (6,10-a)-\max (1,5-a)+1=\sum \min (6,10-a)-\max (0,4-a)=$

$=\frac 1 {216}(3+4+5+6+5+4)=\frac {27}{216} $.

Not sure that is easier or quicker. The max and min values make it hard to generalize.

Answer 6

Hint Show that the number of combinations with sum $n$ is just the coefficient of $x^n$ in $$(x+x^2+x^2+x^4+x^5+x^6)^3$$