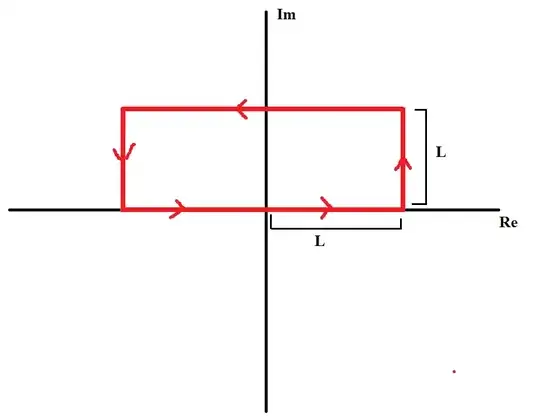
I understand that when we have a polynomial a semicircle is used because the poles are included in the contour when doing so but in the following example a rectangle has been used and I am struggling to understand how to come up with this i.e. what the reasoning behind it is.
10.3.2 Computing $\widehat{f}(\xi)$, and hence $\phi(\xi, x)$, by using the CRT:
Next we are going to show that the function $f: \mathbb{R}^{1} \rightarrow \mathbb{R}^{1}, f(x)=\operatorname{sech}(\pi x)$, has Fourier transform $$ \hat{f}(\xi)=\operatorname{sech}(\xi / 2), \quad \xi \in \mathbb{R}^{1} $$ To do that, consider the contour integral $$ \int_{\gamma_{n}} e^{i \xi z} \operatorname{sech}(\pi z) d z \quad \text { with } \xi>0 $$ around the finite rectangle $\gamma_{n}$ in $\mathbb{C}=\{x+i y\}$ bounded by the lines $$ y=0, \quad y=n+1, \quad x=-n-1, \quad x=n+1 $$ with $n$ a positive integer.