Area bounded by $\cos x+\cos y=1$

Question

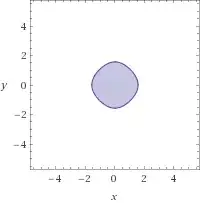
What is the area of the region $\cos x+\cos y > 1$, where $|x|,|y|<\pi$?

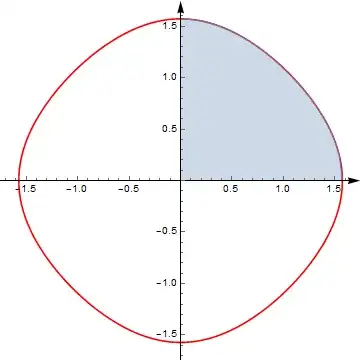
In other words, is there a "closed" form -- using functions that are well-known and nice to work with -- for this integral? $$4\int_0^{\pi/2}\cos^{-1}(1-\cos x)\,dx = 7.2948823845\ldots$$

I can approximate it pretty well:

>>> scipy.integrate.quad(func=lambda x: math.acos(1-math.cos(x)),
...                      a=0, b=math.pi/2,
...                      epsabs=1e-14, epsrel=1e-13, limit=200)
(1.8237205961260357, 1.0436096431476471e-14)

times 4:

(7.294882384504143, 4.1744385725905886e-14)

These numbers don't appear in Inverse Symbolic Calculator, OEIS, or Google.

I ask this question because finding the area of $(\cos x + \cos y > M)$ for a variable $M$ is an intermediate step towards a solution to this question: What is the chance that an $n$-gon whose vertices lie randomly on a circle's circumference covers a majority of the circle's area? I figure that if there's any chance that this area is a reasonable function of $M$, then it should have a reasonable value when $M=1$!

Edit: In the comments, LCFactorization found this form: $$\frac{8}{9\sqrt{\pi}}\left( 9\Gamma\left(\frac{3}{4}\right)^2{}_4F_3\left( \begin{array}{c}\frac14,\frac14,\frac34,\frac34\\\frac12,\frac54,\frac54\end{array};\frac14\right) + \Gamma\left(\frac{5}{4}\right)^2{}_4F_3\left( \begin{array}{c}\frac34,\frac34,\frac54,\frac54\\\frac32,\frac74,\frac74\end{array};\frac14\right) \right)$$ How can we humans derivate that expression from the integral? And can it be simplified?

Edit²: And how can one get a symbolic integration engine to handle such an integral? In Mathematica, the inputs Integrate[ Boole[Cos[x] + Cos[y] > 1], {x, -Pi/2, Pi/2}, {y, -Pi/2, Pi/2}] and Integrate[ArcCos[1 - Cos[x]], {x, 0, Pi/2}] just output integrals again. How do you hint to it to try crazy hypergeometric functions?

Answer 1

Write the implicit equation into parametric form: $$\begin{cases} x(t)=t\\ y(t)=\pm\arccos(1-\cos t) \end{cases}\quad t\in [-\dfrac{\pi}2,\dfrac{\pi}2]\tag{1}$$

The curve looks like:

Use Green's theorem,

$${\rm Area}=4\int_0^{\tfrac{\pi}2}x(t){\rm d}y(t)=4\int_0^{\tfrac{\pi}2}\dfrac{-t \;\sin t\; {\rm d}t}{\sqrt{(2-\cos t) \cos t}}\tag{2}$$

Substitute $u=\cos t$, $t=\arccos u$:

$${\rm Area}=4\int_0^1 \dfrac{\arccos u}{\sqrt{2 u-u^2}}{\rm d}u \tag{3}$$

Then calculate (3) in Mathematica you can obtain the desired output:

(1/(9 Sqrt[[Pi]]))8 (9 Gamma[3/4]^2 HypergeometricPFQ[{1/4, 1/4, 3/4, 3/4}, {1/2, 5/4, 5/4}, 1/4] + Gamma[5/4]^2 HypergeometricPFQ[{3/4, 3/4, 5/4, 5/4}, {3/2, 7/4, 7/4}, 1/ 4])