Length of tangents to general conic section from an external point

Question

Suppose $f(x, y) =0$ represents a conic section, then $\sqrt{f(a, b)} =\sqrt{S_{11}} $ is the length of tangents drawn to conic drawn from point $(a, b) $

This can be easily done for circle but after that I have no idea where this is coming from and it's giving me an headache. It's given in my textbook without proof.

Answer 1

Given the conic equation $a_{11} x^2 + a_{22} y^2 + 2a_{12}xy + 2a_{13} x + 2a_{23} y + a_{33} = 0 $

The conic is non-degenerate if the determinant of the symmetric matrix $a_{ij}=a_{ji}$ is not zero

$$A=\left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{array} \right|\ne 0$$

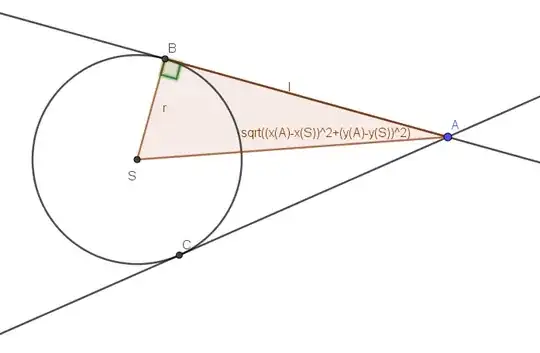
you can write the equation of the polar line from an external point $P(x_0,y_0)$

$$(a_{11} x_0 + a_{12} y_0 + a_{13} )\,x + (a_{21} x_0 + a_{22} y_0 + a_{23} )\,y + a_{31} x_0 + a_{32} y_0 + a_{33} = 0$$

This line intersects the conic in the points where the tangents do, so you can solve the system between the conic and the polar and find the distances from the intersection points to the point $P$

In the example of Jan Magnus we had

$x^2-xy+y^2-1=0$ so that $a_{11}=1;\;a_{12}=a_{21}=-\frac12;\;a_{22}=1;\;a_{33}=-1$

and the point is $P(-2,0)$

Thus the polar line has equation

$-2x + \left(-\frac12 (-2) \right)\,y -1= 0 $ that is $y=2x+1$

plug this equation in the equation of the conic, to solve the system

$x^2-x(2x+1)+(2x+1)^2-1=0$ that is $3 x^2+3 x=0$ which gives $x_1=0;\;y_1=1$ and $x_2=-1;\;y_2=1$ Intersection points are $A(0,1)$ and $B(-1,1)$

We find $PA=\sqrt 5$ and $PB=\sqrt 2$

Hope this helps

Answer 2

The general nondegenerate conic

Consider the conic $s=ax^2+b(xy+yx)+cy^2+d(x+x)+e(y+y)+f=0,$ under the assumption that it is nondegenerate, and the polar wrt pole $A$ then is $s_1=axx(A)+b(xy(A)+yx(A))+cyy(A)+d(x+x(A))+e(y+y(A))+f=0,$ by Joachimsthal. Let's intersect them. The first element in a lex grobner basis is a univariate polynomial in $y:$

$((ab^2-a^2c)x(A)^2+(2b^3-2abc)x(A)y(A)+(b^2c-ac^2)y(A)^2+(2b^2d-2acd)x(A)+(2b^2e-2ace)y(A)-cd^2+2bde-ae^2)y^2+\\((2abd-2a^2e)x(A)^2+(4b^2d-4abe)x(A)y(A)+(2bcd-2ace)y(A)^2+(4bd^2-4ade)x(A)+(2cd^2-2ae^2+2b^2f-2acf)y(A)+2bdf-2aef)y+\\(ad^2-a^2f)x(A)^2+(2bd^2-2abf)x(A)y(A)+(2bde-ae^2-b^2f)y(A)^2+(2d^3-2adf)x(A)+(2d^2e-2aef)y(A)+d^2f-af^2=0$

that together with the polar generally determines $B, C$ the two tangency points. Now the square root taken when solving this is of $-s_{11}\det{\begin{pmatrix}a&b&d\\b&c&e\\d&e&f\end{pmatrix}},$ (where $s_{11}=ax(A)^2+b(x(A)y(A)+y(A)x(A))+cy(A)^2+d(x(A)+x(A))+e(y(A)+y(A))+f$ by Joachimsthal notations again) and the lengths are $AB=\sqrt{(x(A)-x(B))^2+(y(A)-y(B))^2}$ and $AC=\sqrt{(x(A)-x(C))^2+(y(A)-y(C))^2}.$

The circle

That the two equal lengths, $l,$ of the tangents from an external point $A$ are $l=\sqrt{s_{11}}=\sqrt{(x(A)-d)^2+(y(A)-e)^2-r^2}$ certainly is true for circles $(x-d)^2+(y-e)^2-r^2=0,$ as we can see from using Pythagoras on the triangle with the length, $l,$ and $r$ as legs to get $(x(A)-d)^2+(y(A)-e)^2=l^2+r^2.$

The example from the comments

Now consider the case $x^2-xy+y^2-1=0$ it scales to $\frac34s_{11}$ and the whole expression is $-\frac34 y^2+\frac32y(A)y-\frac34y(A)^2=0$ which together with the polar $-\frac12(x y(A)+x(A)y)+y y(A)+x x(A)-1$ defines the ideal $\langle y^2-2y(A)y+y(A)^2, (2x(A)-y(A))x+(-x(A)+2y(A))y-2\rangle$ or in the case of $A=(-2,0)$ $\langle y^2,-4x+2y-2\rangle$ which highlights we sometimes do need more elements from the grobner basis. The next is $-\frac12(3y^2+y-2x-4)=0$ a parabola which together with the polar picks out the two tangency points. But for most $A$ we can get away with $\langle -\frac34 y^2+\frac32y(A)y-\frac34y(A)^2,-\frac12(x y(A)+x(A)y)+y y(A)+x x(A)-1\rangle$ to find $B, C.$ The lengths would have $\sqrt{s_{11}}$ in there, but non-obviously.

In conclusion:

1. Scale the equation $s=0$ hence also $s_1, s_{11}$ by the determinant of the corresponding matrix.
2. For a circle with $a=c=1, b=0$ the square root is taken of $s_{11},$ since $r^2$ is the scale factor (real when the equation comes from $(x-d)^2+(y-e)^2-r^2=0,$ i.e. with $r^2=-(f-d^2-e^2)\geq 0)$ and the lengths are actually $\sqrt{s_{11}}$ as seen above.
3. The general pattern is so unclear as to render any method gleaned from it to be more of a bother than the above method to just find the tangency points by intersecting the polar and the conic and explicitly calculating the lengths.