Is there a geometric method to show $\sin x \sim x- \frac{x^3}{6}$

Question

I found a geometric method to show $$\text{when}\; x\to 0 \space , \space \cos x\sim 1-\frac{x^2}{2}$$ like below :

Suppose $R_{circle}=1 \to \overline{AB} =2$ in $\Delta AMB$ we have $$\overline{AM}^2=\overline{AB}\cdot\overline{AH} \tag{*}$$and $$\overline{AH}=\overline{OA}-\overline{OH}=1-\cos x$$ when $x$ is very small
w.r.t. * we can conclude $$x^2 \approx 2(1-\cos x) \\\to \cos x \sim 1- \frac{x^2}{2}$$ Now I have two question :
$\bf{1}:$ Is there other idea(s) to prove (except Taylor series) $x\to 0 , \space \cos x\sim 1-\frac{x^2}{2}\\$

$\bf{2}:$ How can show $\sin x \sim x- \frac{x^3}{6}$ with a geometric concept ?

Thanks in advance.

Answer 1

Let assume that for small $x$, $$\sin x = x + a x^2 + bx^3 + O(x^4)\tag{1}$$

In this trigonometric circle we can compute $BC$ in two ways:

First, considering the $ABC$ triangle:

$$BC= \sqrt{AB^2+AC^2}=\sqrt{\sin^2 x+\left(1-\sqrt{1-\sin^2 x}\right)^2}=\\= x+ax^2+\left(b+\frac18\right)x^3+O(x^4) \tag{2}$$ [*]

Second, bisecting the angle $x$:

$$BC = 2 \sin \frac{x}{2}=x+\frac{a}{2} x^2 + \frac{b}{4}x^3 + O(x^4)\tag{3}$$

Equating (2) and (3) we get $a=0$ and $b=-\frac{1}{6}$, that is: $\sin x = x - \frac16 x^3 + O(x^4)$

I'm not sure if this a geometric proof, though...

---

[*] To prove (2) we only need to know the expansion, for $t\to 0$: $$\sqrt{1+t}=1+\frac{t}{2}+\cdots \tag{4}$$ (here and in the following expansions the dots means a remainder $O(t^{k+1})$ where $k$ is the highest exponent in the preceeding terms).

Then $$\sqrt{1-t^2}=1-\frac{t^2}{2}+\cdots \\ (1-\sqrt{1-t^2})^2=\frac{t^4}{4}+\cdots\\ t^2+(1-\sqrt{1-t^2})^2=t^2(1+\frac{t^2}{4}+\dots)\\ \sqrt{t^2+(1-\sqrt{1-t^2})^2}=t (1+\frac{t^2}{8}+\cdots) =t +\frac{t^3}{8}+\cdots $$ Letting $t=x+ax^2+bx^3+O(x^4)$ that gives

$$ x+ax^2+bx^3+\frac{x^3}{8}+O(x^4)$$

With some more work (I've verified it with Maxima), doing higher order expansions we can get more terms ($\sin x = x -\frac16 x^3 + \frac{1}{120}x^5 +\cdots$).

Answer 2

Use the formula: $$\sin(a+b)=\sin(a) \cos (b)+\sin(b) \cos (a) \quad (1)$$ Which has a geometrical derivation, to find out $\sin(x)$ in function of $\sin(\frac{x}{3})$. That produces the triple angle formula: $$\sin(x)=3\sin(\frac{x}{3})-4(\sin(\frac{x}{3}))^3 \quad(2)$$ Using the approximation: $$\sin(\frac{x}{9})=\frac{x}{9} \quad (3)$$ And (2) twice, first to get $\sin(\frac{x}{3})$ and after that to get $\sin(x)$, you will get a polynomial: $$\sin(x)=x-\frac{40}{243}x^3 + \text {ninth degree polynomial} \quad (4)$$ The polynomial can be approximated to: $$\sin(x)=x-\frac{1}{6}x^3 $$.

Answer 3

This answer uses another approach. We can approximate the area of a circular segment to an area of a parable. See the picture below.

The area of a circular segment can be calculated by: $$A=\frac{R^2}{2}(\theta-\sin(\theta)) \tag{1}$$

The area of a parable between its zeroes $x_1$ and $x_2$ can be calculated by: $$A=\frac{2}{3}(x_2-x_1)y_{max} \tag{2}$$ where $y_{max}$ is the maximum ordinate of the parable.

If we use: $$x_2 =\sin(\frac{\theta}{2}) \tag{3}$$ $$x_1 =-\sin(\frac{\theta}{2}) \tag{4}$$ $$y_{max}=1-\cos(\frac{\theta}{2})= 2 (\sin(\frac{\theta}{4}))^2 \tag{5}$$ $$\sin(\frac{\theta}{2}) \sim \frac{\theta}{2} \tag{6}$$ $$\sin(\frac{\theta}{4}) \sim \frac{\theta}{4} \tag{7}$$ and $$R=1 \tag{8}$$ in equations (1) and (2) and after that we make the approximation that (1) and (2) are the same, we get: $$\sin(\theta) \sim \theta - \frac{\theta^3}{6}.$$

Answer 4

Now a full answer (assuming we have a result slightly stronger than yours, that $\cos x = 1-\frac{x^2}{2}+o(x^2)$, which is the true meaning of $\cos x\sim 1-\frac{x^2}{2}$, but which you haven't proven - you haven't come up with a bound for your error.)

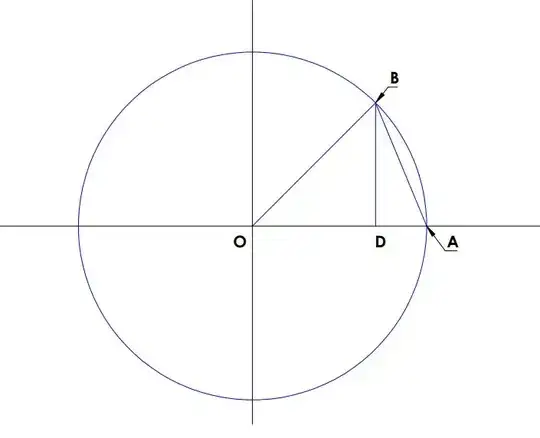
Let $D$ be the midpoint of the arc in $MA$. The area of the quadrilateral $OMDA$ is $\frac{\sin(x)}{2}$.

The area of circular wedge between $M$ and $A$ is $\frac{x}{2}$.

Taking the tangents to the circle at $M$ and $A$ and finding their intersection, $C$, you get that the are of $OMCA$ is $2\tan(x/2)$. So you have:

$$\sin\frac{x}{2}<\frac{x}{2}<\tan\frac{x}{2}$$

Setting $u=\frac{x}{2}$ you get:

$$\sin u< u < \frac{\sin u}{\cos u}$$

Or $\cos u<\frac{\sin u}{u}<1$

This is enough to see that $\sin u = u+O(u^3)$ (using that $\cos(u)=1+O(u^2)$,) but not enough to show what you want.

The goal is to find and approximation of the difference $u-\sin u$, twice the area of the region between the line segment $AD$ and the arc $AD$.

---

Letting $$A_n=\frac{1}2\sin \frac{x}{2^{n}},$$ is the area of $2^{n}$ copies of the triangle $MOA$ with angle $\frac{x}{2^n}$. From this, we see that $2^{n}A_n<\frac{x}{2}$, since the $2^n$ triangles fit inside the wedge.

Now, $A_{n+1}$ is gotten by taking half of the triangle for $A_{n+1}$ and adding a triangle with base $\sin(x/2^{n+1})$ and height $1-\cos(x/2^{n+1})$.

So: $$A_{n+1}=\frac{A_n}{2}+\frac{1}{2}\sin(x/2^{n+1})(1-\cos(x/2^{n+1})).$$

So if $B_{n}=2^{n}A_n$, then $B_0=\frac{\sin x}{2}$ and $$B_{n+1}=B_n+2^{n}\sin(x/2^{n+1})(1-\cos(x/2^{n+1})).$$

Writing $f(x)=x-\sin x$ and $g(x)=\cos x-1+\frac{x^2}{2}$ as our error functions. We get:

$$\begin{align}B_{n+1}-B_{n}&=2^{n}\sin(x/2^{n+1})(1-\cos(x/2^{n+1}))\\&=2^{n}\left(\frac{x}{2^{n+1}}+f\left(\frac{x}{2^{n+1}}\right)\right) \left(\frac{x^2}{2^{2n+3}}+g\left(\frac{x}{2^{n+1}}\right)\right)\\ &=\frac{x^3}{2^{2n+4}}+\frac{x}{2}g\left(\frac{x}{2^{n+1}}\right)+\frac{x^2}{2^{n+3}}f\left(\frac{x}{2^{n+1}}\right)+f\left(\frac{x}{2^{n+1}}\right)g\left(\frac{x}{2^{n+1}}\right) \end{align}$$

Now, we know that $f(x)=O(x^3)$ and $g(x)=o(x^2)$, so we get:

$$\begin{align}\lim_{n\to\infty} B_n &= B_0+\sum_{n=0}^{\infty}\left(B_{n+1}-B_n\right)\\ &=\frac{\sin x}{2}+\left(x^3\sum_{n=0}^{\infty}\frac{1}{2^{2n+4}}\right)+o(x^3)+O(x^5)+o(x^5)\\ &=\frac{\sin x}{2}+\frac{x^3}{12}+o(x^3) \end{align}$$

But $\lim_{n\to\infty} B_n =\frac{x}{2}$, because this is the area of the circular wedge.

So we have: $$x-\sin x = \frac{x^3}{6} + o(x^3)$$

---

You can actually prove that $B_n\to \frac{x}{2}$ by noting that $\frac{B_{n}}{\cos(x/2^n)}$ is the area of $2^n$ triangles that cover the circular wedge, and thus you have:

$$B_n<\frac{x}{2}<\frac{B_n}{\cos(x/2^n)}$$

Simce $B_n$ is increasing, and $\cos(x/2^n)\to 1$, we see that both values converge to $\frac{x}{2}$.

---

The full proof first prove that $\sin x = x+o(x)$.

From this, though, we can show that:

$$\cos(x)=1-2\sin^2 \frac{x}{2} = 1-\frac{x^2}{2}+o(x^2).$$

Then the rest of the argument follows, since $\cos(x)=1+O(u^2)$.

Answer 5

Not a complete answer, I am afraid. Approximating the arc $AB$ as a line segment leads to the correct approximation of $\cos(x) \sim 1 - \frac{x^2}{2}$ but leads to the inaccurate result for the corresponding sine as $ \sin(x) \sim x - \frac{x^3}{8}$. Nevertheless, I post my approach, since it has not been covered in the preceding answers.

In the above diagram, we have $OA=OB=1$ and $\angle BOA = x$

Let the co-ordinates of point $B$ be $(h,k)$

Since $B$ lies on the unit circle, $$h^2 + k^2 =1\tag{1}$$ The equation of the line $AB$ is given as $y^*=m(x^*-1)$ and since B lies on the line $AB$, we have $$ k=m(h-1\tag{2})$$ where $m$ is the slope of $AB$.

From $(1)$ and $(2)$, we have $$\Rightarrow h^2 + m^2(h-1)^2=1 $$ $$\Rightarrow h^2(1+m^2) - h(2m^2) + (m^2 -1)=0 $$ which gives two values of $h$, of which one value $h=1$ is for the point $A$ $$\Rightarrow h=\frac{m^2 -1}{m^2 +1}, \; k =\frac{-2m}{m^2 +1} \tag{3}$$

The length of the line segment $AB$ is assumed to be $x$, hence $$\Rightarrow (h-1)^2 + k^2 =x^2 \tag{4}$$

Using $(2)$ and $(4)$, we get $$ \Rightarrow (1+m^2)(h-1)^2 =x^2$$ $$\Rightarrow x=|h-1|\sqrt{1+m^2}=(1-h)\sqrt{1+m^2}$$ From $(3)$, we have $$ \Rightarrow x=\frac{2}{\sqrt{1+m^2}}$$ $$ \Rightarrow 1+m^2 = \frac{4}{x^2}$$ $$ \Rightarrow m = \sqrt{\frac{4-x^2}{x^2}} \tag{5}$$

Now, using $(5)$ and $(3)$, $$ h=OD=\frac{4-2x^2}{4}, \; k=DB= \frac{x\sqrt{4-x^2}}{2}$$

Thus $OD = \cos(x) \sim 1-\frac{x^2}{2}$ and $DB= \sin(x) \sim x(1-\frac{x^2}{4})^{1/2}$

This gives $\sin(x) \sim x - \frac{x^3}{8}$, which isn't quite correct.

Answer 6

Here is a proof that uses the fact, once in $(4)$ and twice in $(5)$, that $$ \lim_{x\to0}\frac{\sin(x)}{x}=1\tag{1} $$ A geometric proof of $(1)$ can be found in this answer.

---

Answer Using the Duplication Formulas for $\boldsymbol{\sin(x)}$ and $\boldsymbol{\cos(x)}$

Using the duplication formulas for $\sin(x)$ and $\cos(x)$, we get $$ \begin{align} \frac{2\sin(x/2)-\sin(x)}{x^3} &=\frac{2\sin(x/2)-2\sin(x/2)\cos(x/2)}{x^3}\\ &=\frac{2\sin(x/2)}x\,\frac{1-\cos(x/2)}{x^2}\\ &=\frac{2\sin(x/2)}x\,\frac{2\sin^2(x/4)}{x^2}\tag{2} \end{align} $$ Substituting $x\mapsto\frac{x}{2^k}$ in $(2)$ gives $$ \frac{2^{k+1}\sin\left(\frac{x}{2^{k+1}}\right)-2^k\sin\left(\frac{x}{2^k}\right)}{x^3}=4^{-k}\frac{2\sin\left(\frac{x}{2^{k+1}}\right)}{\frac{x}{2^k}}\,\frac{2\sin^2\left(\frac{x}{2^{k+2}}\right)}{\frac{x^2}{4^k}}\tag{3} $$ Summing in $k$, the left side of $(3)$ telescopes: $$ \frac{x-\sin(x)}{x^3}=\sum_{k=0}^\infty4^{-k}\frac{2\sin\left(\frac{x}{2^{k+1}}\right)}{\frac{x}{2^k}}\,\frac{2\sin^2\left(\frac{x}{2^{k+2}}\right)}{\frac{x^2}{4^k}}\tag{4} $$ Since the terms of the right side of $(4)$ are dominated by $\frac18\cdot4^{-k}$, Dominated Convergence yields $$ \begin{align} \lim_{x\to0}\frac{x-\sin(x)}{x^3} &=\sum_{k=0}^\infty4^{-k}\lim_{x\to0}\frac{2\sin\left(\frac{x}{2^{k+1}}\right)}{\frac{x}{2^k}}\,\lim_{x\to0}\frac{2\sin^2\left(\frac{x}{2^{k+2}}\right)}{\frac{x^2}{4^k}}\\ &=\frac43\cdot1\cdot\frac18\\[6pt] &=\frac16\tag{5} \end{align} $$

---

Answer Inspired by Equation $\boldsymbol{(2)}$ from Ricardo Cruz's Answer

Recall the triplication formula for $\sin(x)$: $$ \sin(3x)=3\sin(x)-4\sin^3(x)\tag{6} $$ Substituting $x\mapsto\frac{x}{3^{k+1}}$ gives $$ \frac{3^{k+1}\sin\left(\frac{x}{3^{k+1}}\right)-3^k\sin\left(\frac{x}{3^k}\right)}{x^3}=4\cdot9^{-k}\frac{\sin^3\left(\frac{x}{3^{k+1}}\right)}{\frac{x^3}{27^k}}\tag{7} $$ Summing in $k$, the left side of $(7)$ telescopes: $$ \frac{x-\sin(x)}{x^3}=\sum_{k=0}^\infty4\cdot9^{-k}\frac{\sin^3\left(\frac{x}{3^{k+1}}\right)}{\frac{x^3}{27^k}}\tag{8} $$ Since the terms of the right side of $(8)$ are dominated by $\frac4{27}\cdot9^{-k}$, Dominated Convergence yields $$ \begin{align} \lim_{x\to0}\frac{x-\sin(x)}{x^3} &=\sum_{k=0}^\infty4\cdot9^{-k}\lim_{x\to0}\frac{\sin^3\left(\frac{x}{3^{k+1}}\right)}{\frac{x^3}{27^k}}\\ &=4\cdot\frac98\cdot\frac1{27}\\[6pt] &=\frac16\tag{9} \end{align} $$