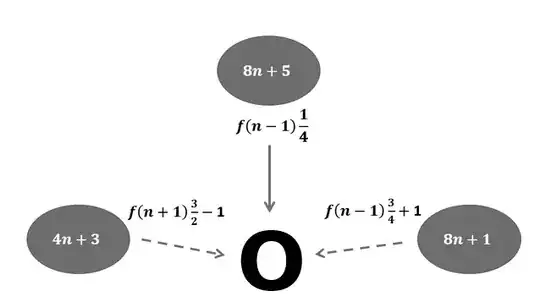
There are two injective functions and one bijective function that map all sequences, without exception - and that explains the lattice pattern:
The injective functions are:
For every $4n+3: f(n+1)\frac{3}{2}-1$
3→5, 7→11, 11→17, 15→23, 19→29, 23→35, 27→41, 31→47
For every $8n+1: f(n−1)\frac{3}{4}+1$
1→1, 9→7, 17→13, 25→19, 33→25, 41→31, 49→37, 57→43
The input numbers are disjoint. But the output numbers of the two injective functions must be convergent with the output numbers of the bijective function (unless a multiple of $3$).
The bijective function is for every $8n+5: f(n−1)\frac{1}{4}$
5→1, 13→3, 21→5, 29→7, 37→9, 45→11, 53→13, 61→15
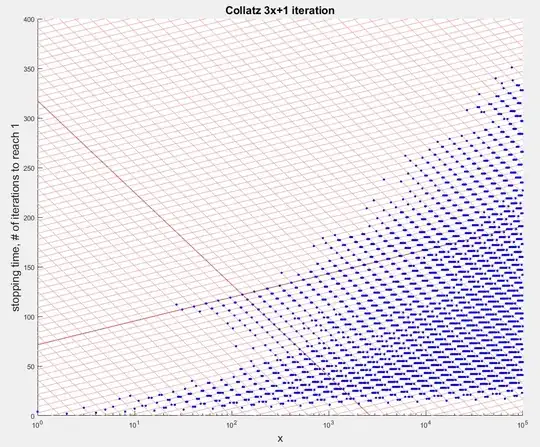
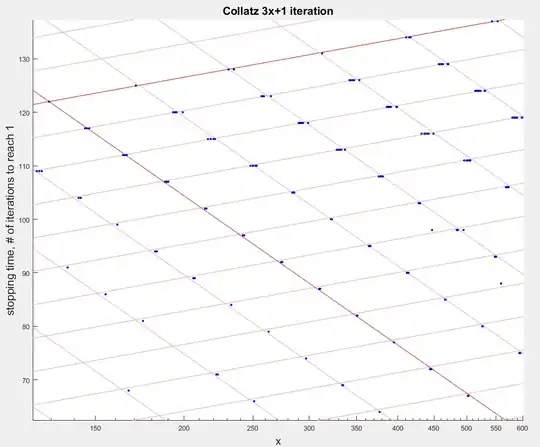
While it's obvious that if you multiply $4n+1$ by $3n+1$ – that is, $(((n*4)+1)3)+1$ – you add two factors of $2$, it's less than obvious that this is occurring in even-odd sequences, as you do not see the repetition of the first odd $n$ in such related sequences. For example:
31 → 94 → 47
125 → 376 → 188 → 94 → 47
501 → 1504 →752 → 376 → 188 → 94 → 47
Nevertheless, it is true - the convergence occurs on an even number.
If you put these three functions together, they must account for the odd-numbered proper superset of even-odd sequences. That is, all sequences can be projected to converge, using these functions, beginning with the basis case: 1 --> 1, 5 --> 1. It should be possible by induction to show there can be no "infinite" sequence excepting a nontrivial loop - and the logic to support this possibility is scant given the interrelatedness of the aforementioned functions. I don't see an alternative conclusion.