I've recently starting reading about number theory, and came across this proposition in A Classical Introduction to Modern Number Theory:
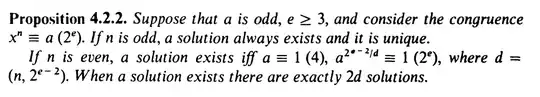 The hint is to start writing $x$ and $a$ as $(-1)^y5^z$ and $(-1)^s5^t$ respectively. For the first case where $n$ is odd, I have:
The hint is to start writing $x$ and $a$ as $(-1)^y5^z$ and $(-1)^s5^t$ respectively. For the first case where $n$ is odd, I have:
$x^n \equiv (-1)^{yn}5^{zn} \equiv (-1)^{y2k}(-1)^y5^{zn} \equiv (-1)^y5^{zn}$
where the third step occurs from writing $n = 2k + 1$ for some $k$. Thus we are left with the relation:
$(-1)^y5^{nz} \equiv (-1)^s5^t (2^e)$
but I'm not quite sure where to go from there, any advice would be great, thanks!