4

Disclaimer: This is a cross-post from stackoverflow -- the community recommended to post it here again

I want to calculate the distance from a point given by latitude and longitude to a line-segment given by two points (part of a great-circle). All coordinates are given in WGS84.

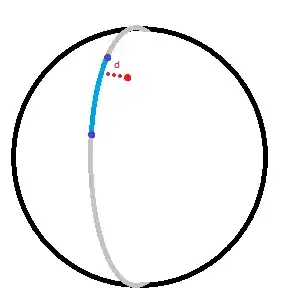
point-great-circle-arc-distance

I know how to calculate this in cartesian coordinates but not on a sphere. Can somebody please provide the formula?

Henry
  • 157,058
user2033412
  • 141
  • 1
    But WGS84 models the earth as an ellipsoid, not a sphere. – kimchi lover Aug 09 '17 at 11:01
  • I guess if we can estimate the error "far enough away" from the poles we can reduce it to a sphere for my special case. :-) – user2033412 Aug 09 '17 at 11:03
  • In the spherical fictional world: Work out the $(x,y,z)$ coordinates of the 3 points in a coordinate system that puts the center of the earth at $(0,0,0)$. Call the 2 points determining the great circle $A$ and $B$, call the other point $P$. Thinking of them as vectors in $\mathbb R^3$, you want the angle between $P$ and the cross product $A\times B$. Multiply that angle by the radius of the earth, and there you are. – kimchi lover Aug 09 '17 at 11:32
  • But what if the projected point lays not within the arc but outside of it? – user2033412 Aug 09 '17 at 11:43
  • You're right. It's what I said, or the GS distance to $A$, or the GS distance to $B$, and the rule for deciding which can be based on other obvious angle inequalities. – kimchi lover Aug 09 '17 at 11:48
  • See https://math.stackexchange.com/questions/337055/compute-minimum-distance-between-point-and-great-arc-on-sphere/2627920. – Louis Strous Jan 30 '18 at 12:24

1 Answers1

0

I refer to the figure provided by OP and call the given base point the red point and the segment marked blue on the great circle the blue target (curved) segment.

Based on comments I suppose OP approves the assumption of spherical shape of the earth. Therefore, the radius $R$ of the earth is taken to be constant everywhere.

It makes the problem easy to know that the two ends of the blue target (curved) segment are on the same meridian. This means that the sought perpendicular is a segment on the latitudinal circle that passes through the red point. Specifically, we are looking for the length of a (curved) segment on the latitudinal circle of the red point, bounded between the longitudes of the red point and the blue target (curved) segment.

The radius of the said longitudinal circle is $$r = R cos {\beta} $$ where $\beta$ is the red point's latitude.

The length of the sought perpendicular is then $$s = r(\Delta \alpha) $$ where $\Delta \alpha$ is the difference between longitudes of the red point and the blue target (curved) segment.

Saeed
  • 1,872