Hello Good day everyone,
Can everyone help me with this problem.
From a circular piece of metal sheet with diameter $20 \text{cm}$ a rectangular piece with perimeter $28\text{cm}$ is to be cut. Find the dimensions of the rectangular piece.
I tried answering this one but I have doubts if I am going to use the system with equation $x^2+y^2=20^2$ and $x+y=14$. And as I evaluate the system, it leads to a imaginary numbers.
Thank you for the response!
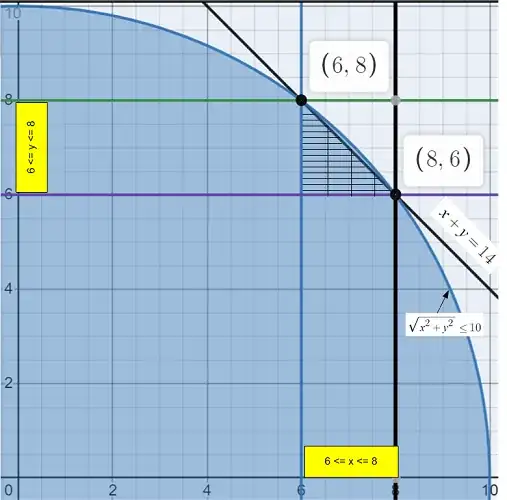
lets say that both the circle and rectangle are at the same centre, my answer is best understood if visualized, in the rectangle the length " $b$ " is horizontal and the breath " $a$ " is vertical
we know that the perimeter $2(a+b)$ of the rectangle is $28$, then $a+b = 14$ and the circle has a diameter of $28$, then it's area is $\pi \cdot (20/2)^2$
obviously the area of the rectangle has to be less than the circle, since it was cut from it, then $a\cdot b < \pi \cdot 10^2$ and $b = 14-a$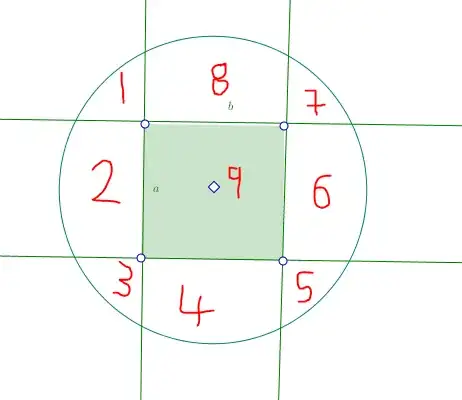
interpreting the maths from my diagram, the circle $!(1,2,3,4,5,6,7,8,9)$ is cut into $9$ parts, according to my theory we would use the information to extract the dimension of the rectangle
so that area of the circle $!(1,2,3,4,5,6,7,8,9)$ equals area of the rectangle $!(9)$ plus area of the eclipse $!(1,2,3,5,6,7)$ plus area of the second eclipse $!(1,3,4,5,7,8)$ minus area of the sector $!(1)$ minus area of the sector $!(3)$ minus area of the sector $!(5)$ minus area of the sector $!(7)$
hehe, because a cicrcle has a perfect regular shape, the area of the sector $!(1)$ equals sector $!(3)$ equals sector $!(5)$ equals sector $!(7)$, this sector is the sector of some eclipse
we have to find the two radius of the eclipse $!(1,2,3,5,6,7)$ which is $$ R_{a} = \sqrt{10^2-(\frac{b}{2})^2 } $$ $$ R_{b} = \frac{20-b}{2}$$ the radius of the second eclipse $!(1,3,4,5,7,8)$ is $$ r_{a} = \frac{20-a}{2}$$ $$ r_{b} = \sqrt{10^2-(\frac{a}{2})^2}$$ the radius of the sector at the edge is also calculated, sector $!(1)$=$!(3)$=$!(5)$=$!(7)$ $$ ( R_{a} - \frac{ a}{2} )$$ and $$ ( r_{b} - \frac{ b}{2} )$$ area of circle $!(1,2,3,4,5,6,7,8,9)$ = area of rectangle $!(9)$ + area of eclipse $!(1,2,3,5,6,7)$ + area of eclipse $!(1,3,4,5,7,8)$ - 4 * area of sector $!(1)$
$$ \pi \cdot 10^2 = a b + \pi \cdot R_{a} \cdot R_{b} + \pi \cdot r_{a} \cdot r_{b} - 4 \cdot \frac{1}{4} \cdot \pi \cdot ( R_{a} - \frac{ a}{2}) \cdot ( r_{b} - \frac{ b}{2}) $$
$$ \pi \cdot 10^2 = a b + \frac{ \pi (20-b) \cdot \sqrt{10^2-\frac{b}{2}^2} }{2} + \frac{ \pi (20-a) \cdot \sqrt{10^2- \frac{a}{2}^2 }}{2} - 4 \cdot \frac{1}{4} \cdot \pi \cdot ( \sqrt{10^2-\frac{b}{2}^2 } - \frac{a}{2} )\cdot ( \sqrt{10^2-\frac{a}{2}^2 } - \frac{b}{2} )$$
$$ \pi \cdot 10^2 = a b + \frac{ \pi (20-b) \cdot \sqrt{10^2-\frac{b}{2}^2} }{2} + \frac{ \pi (20-a) \cdot \sqrt{10^2-\frac{a}{2}^2 }}{2} - \pi \cdot \sqrt{10^2-\frac{b}{2}^2} \cdot \sqrt{10^2-\frac{a}{2}^2 } + \pi \cdot \frac{b}{2} \cdot \sqrt{10^2-\frac{b}{2}^2} + \pi \cdot \frac{a}{2} \cdot \sqrt{10^2-\frac{a}{2}^2} - \pi \cdot \frac{a \cdot b}{4} $$
$$ \pi \cdot 10^2 - a b + \pi \cdot \frac{a b}{4} + \pi \cdot \sqrt{10^2-\frac{b}{2}^2} \cdot \sqrt{10^2-\frac{a}{2}^2 } = \frac{ \pi (20-b) \cdot \sqrt{10^2-\frac{b}{2}^2} }{2} + \frac{ \pi (20-a) \cdot \sqrt{10^2-\frac{a}{2}^2} }{2} + \pi \cdot \frac{b}{2} \cdot \sqrt{10^2-\frac{b}{2}^2} + \pi \cdot \frac{a}{2} \cdot \sqrt{10^2-\frac{a}{2}^2} $$
$$ (\pi\cdot 10^2 - a b + \pi \cdot \frac{a \cdot b}{4} + \pi \cdot \sqrt{10^2-\frac{b}{2}^2} \cdot \sqrt{10^2-\frac{a}{2}^2 } )^2 = ( \frac{ \pi (20-b) \sqrt{10^2-\frac{b}{2}^2} }{2} + \frac{ \pi (20-a) \cdot \sqrt{10^2-\frac{a}{2}^2} }{2} + \pi \cdot \frac{b}{2} \cdot \sqrt{10^2-\frac{b}{2}^2} + \pi \cdot \frac{a}{2} \cdot \sqrt{10^2-\frac{a}{2}^2} )^2 $$
$$ (\pi \cdot 10^2 - a b + \pi \cdot \frac{a b}{4} + \pi \cdot \sqrt{10^2-\frac{b}{2}^2} \cdot \sqrt{10^2- \frac{a}{2}^2 }{2} )^2 - ( \frac{ \pi (20-b) \sqrt{10^2-\frac{b}{2}^2 }}{2} + \frac{ \pi (20-a) \cdot \sqrt{10^2-\frac{a}{2}^2 }} + \pi \frac{b}{2} \cdot \sqrt{10^2-\frac{b}{2}^2} + \pi \cdot \frac{a}{2} \cdot \sqrt{10^2-\frac{a}{2}^2} )^2 = 0 $$
$$ -\frac{a \cdot \sqrt{100-\frac{a^2}{4}} \cdot b \cdot \sqrt{100-\frac{b^2}{4} } \cdot \pi^2 }{2} -\frac{a^2 b^2 \pi^2}{8} -50 a b \pi^2 +2 a\cdot \sqrt{100-\frac{a^2}{4}}\cdot b\cdot \sqrt{100-\frac{b^2}{4}}\cdot \pi +\frac{a^2 b^2 \pi}{2} + 200 a b\pi-a^2 b^2 = 0 $$
$$ \frac{ -a b \cdot ( \sqrt{400-a^2}\cdot \sqrt{400-b^2}\cdot \pi^2+a\cdot b\cdot \pi^2+400\cdot \pi^2-4\cdot \sqrt{400-a^2}\cdot \sqrt{400-b^2}\cdot \pi-4 a b\pi-1600 \pi+8a b ) }{8} = 0 $$
$$ \sqrt{400-a^2}\cdot \sqrt{400-b^2}\cdot \pi^2+ab \pi^2+400 \pi^2-4\sqrt{400-a^2}\cdot \sqrt{400-b^2}\cdot \pi-4 a b \pi-1600\pi+8 a b = 0 $$
$$ \sqrt{400-a^2}\cdot \sqrt{400-b^2} \cdot (\pi^2-4\cdot \pi)+(a b+400) \pi^2+(-4 ab-1600) \pi+8 a b = 0 $$
$$ \sqrt{400-a^2}\cdot \sqrt{400-b^2} \cdot (\pi^2-4\cdot \pi) = -(a b+400) \pi^2+(4 a b+1600)\pi -8 a b $$
$$ ( \sqrt{400-a^2}\cdot \sqrt{400-b^2} \cdot (\pi^2-4 \pi) )^2 = ( -(a b+400)\pi^2+(4 a b+1600) \pi -8 a b )^2 $$
$$ ( \sqrt{400-a^2}\cdot \sqrt{400-b^2} \cdot (\pi^2-4 \pi) )^2 - ( -(a b+400) \pi^2+(4 a b+1600) \pi -8a b )^2 = 0 $$
$$ -400b^2\pi^4-800ab\pi^4-400a^2\pi^4+3200b^2\pi^3+6400ab\pi^3+3200a^2\pi^3-16a^2b^2\pi^2-6400b^2\pi^2-19200ab\pi^2-6400a^2\pi^2+64a^2b^2\pi+25600ab\pi-64a^2b^2 = 0 $$ $$ -16( 25b^2\pi^4+50ab\pi^4+25a^2\pi^4-200b^2\pi^3-400ab\pi^3-200a^2\pi^3+a^2b^2\pi^2+400b^2\pi^2+1200ab\pi^2+400a^2\pi^2-4a^2b^2\pi-1600ab\pi+4a^2b^2 ) = 0 $$ $$ 25b^2\pi^4+50ab\pi^4+25a^2\pi^4-200b^2\pi^3-400ab\pi^3-200a^2\pi^3+a^2b^2\pi^2+400b^2\pi^2+1200ab\pi^2+400a^2\pi^2-4a^2b^2\pi-1600ab\pi+4a^2b^2 = 0 $$ $$ 25a^2\pi^4+50(14-a)a\pi^4+25(14-a)^2\pi^4-200a^2\pi^3-400(14-a)a\pi^3-200(14-a)^2\pi^3+(14-a)^2a^2\pi^2+400a^2\pi^2+1200(14-a)a\pi^2+400\pi(14-a)^2\pi^2-4(14-a)^2a^2\pi-1600(14-a)a\pi+4(14-a)^2a^2 = 0$$ $$ 4900\pi^4-39200\pi^3+a^4\pi^2-28a^3\pi^2-204a^2\pi^2+5600a\pi^2+78400\pi^2-4a^4\pi+112a^3\pi+816a^2\pi-22400\pi a\pi+4a^4-112a^3+784a^2 = 0 $$ $$1.303233786730186a^4-36.49054602844518a^3+1334.140307507042a^2-15101.89079431095a+35635.48524426483 = 0$$ $$[a=3.188302332738908,a=10.81169766726106,a=27.28084114342327i+7.000000000000011,a=7.000000000000011-27.28084114342327i]$$ therefore the dimension of the rectangle is $ 3.18 $ by $10.81$
By the formula $2(a+b) = 28$, $a+b=14$, where the sides of the rectangle $a$ and $b$. Since $a,b$ have to be positive, we can conclude that the maximum length of one side is smaller than $14$.
This length is smaller than $20$, the diameter of the circle, so any rectangle that can be possibly cut from the sheet.
As for translating the rectangle, we just have to translate the rectangle up or down until it touches the rectangle. Since there is a point where the rectangle transfers from being fully inside to partially outside, at one point the rectangle must touch the circle exactly.
Let there be a rectangle that is parallel to the $x$-axis, and a circle centred at $(0,0)$. Then, we can find a chord, and thus a rectangle, that intersects the circle at two points (internally).
By some observation, the lines at the top and bottom of the rectangle have equations $y = \frac{b}{2}$ and $y = -\frac{b}{2}$, where $b$ is the length of the chord, and also the top/bottom side of the rectangle.
Since you already have the $y$-coordinates (because they lie on the line), we can use the equality $y=\frac{b}{2}$ and put that value in the equation $x^2+y^2=10^2$ with the two equations to solve for $x$. This should give you the coordinates of the points you need.
The circle with diameter $20$ must have a radius of $10$. To answer your specific question about the use of: $x^2+y^2=20^2$, you don't need this since it is incorrect.
The area of the circle from given data is: $A=\pi r^2=100\pi=314.159$.
Let the rectangle have sides $x$ and $y$. Since the rectangle has to be inside the circle, then the area of the rectangle is less than or equal to the area of the containing circle. Also, the rectangle's diagonal can't be larger than the circle diameter. Accordingly the following relations must be satisfied simultaneously by any valid solution :
$$x+y=14...\left(1\right)$$
and
$$\sqrt{x^2+y^2}\leq10...\left(2\right)$$
and
$$xy\le 314.159...\left(3\right)$$
and
$$0< x,y\leq10$$
You can use (1) and (2) above to find the intersection between the line and the circle to be points $(6,8)$ and $(8,6)$. Hint: $y=14-x$ can be substituted in $(2)$ after squaring both its sides to get: $x^2+\left(14-x\right)^2-100=0$.
From the above and the diagram the solution is any point (x,y) such that: $$ 6<=(x,y)<=8 $$ in addition to the above constraints.
For example:
Points $(6,8)$, $(6.1,7.9)$, $(7,7)$ and $(8,6)$ are part of the solutions set.
Point $(6.1,7.924)$ is not a solution.
Since there are no special rules, just assume that you are cutting a square centered at $(0,0)$ and aligned with the axis. Does it fit inside the circle? Yes, because $3.5^2+3.5^2 = 24.5 \leq 100$. So, an admissible answer is that the cut corresponds to a square with side 7.
We reproduce here the system of equations you have given in your problem text to show that your statement “it led to imaginary numbers” is false. $$x^2+y^2=400\tag{1}$$ $$x+y=1\tag{2}4$$
If we solve for the variable $x$, we get, $$x=7\pm\sqrt{151}.$$
Therefore, what we have here are two real roots. One of them is positive and it is given below. $$x=19.2882.$$ However, the the corresponding $y$ value obtained using (2) is negative i.e., $$y=-5.2882.$$
Therefore, this is not an acceptable solution to your problem. In order to obtain an acceptable solution to this problem, we must express the first equation as, $$x^2+y^2\le 400,$$ which can also be written as, $$x^2+y^2=400-{\large{\delta,}}\qquad\text{where}\quad {\large{\delta}} \gt 0 \tag{3}$$ of which the positive real root is, $$x=7+\sqrt{151-{\large{\delta}}}.\tag{4}$$
We know that, from (2), both $x$ and $y$ are less than 14. Therefore, using (4), we shall write, $$x=7+\sqrt{151-{\large{\delta}}}\lt 14 \qquad{\large{\rightarrow}} \qquad{\large{\delta}}\gt102.$$
At the same time we need to be careful not to make $x$ an imaginary number. This is guaranteed if we chose, $$\sqrt{151-{\large{\delta}}}\ge 0 \qquad{\large{\rightarrow}} \qquad{\large{\delta}}\le 151.$$
You can substitute any value between 102 and 151 in place of ${\large{\delta}}$ in (4) to determine a value of $x$. Once you have $x$, use (2) to obtain the value of $y$.
