We can use limits to differentiate a function using differentiation from first principles
$\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}$
But can we set an equality like
$\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}$ = ${x}$
$\ f(x)=\frac{x^2}{2}$
To integrate a function?
Or using other method without those integration rules for example
$\int{x} dx = \frac{x^2}{2}$
$\int{e^x} dx = e^x $
etc
Just like differentiation from first principles
Do we have similar things in integration?
thank you so much!!
I believe you are asking if integration can be defined in a way other than setting an identity (e.g., with a limit like differentiation). This is how the Riemann integral is defined. The integral is taken as the limit of a Riemann sum:
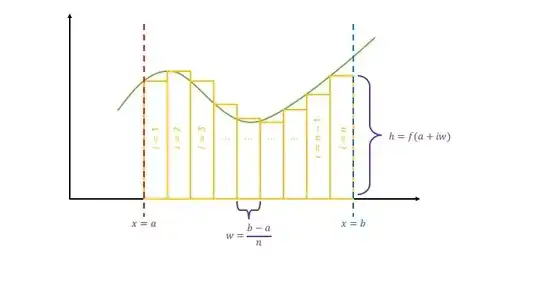
$$\begin{align} \int_a^b f(x) \, dx &= \lim_{n\to\infty}\sum_{i=1}^{n}h \cdot w \\ &= \lim_{n\to\infty}\sum_{i=1}^{n} f\left(a+iw\right) \cdot \frac{b-a}{n} \\ &= \lim_{n\to\infty}\sum_{i=1}^{n} f\left(a+i\frac{b-a}{n}\right) \cdot \frac{b-a}{n} \\ \end{align}$$
If you are an introductory calculus student, this is the type of definite integration that you use. The identities from indefinite integration come from the understanding that determining an antiderivative and evaluating it between two points yields the same value as the limiting process.
As you enter higher levels of math, Riemann integration fails or simply makes no sense. This is when other forms of integration—such as Lebesgue integration, which might be the easiest for you to grasp—must come into play.
Concrete example where the Riemann integral can be calculated as limit of a sum: the function $x\mapsto x^k$, $k\in\Bbb N$. You can prove easily that $$1^k + 2^k + \cdots + n^k = \frac{n^{k+1}}{k+1} + O(n^k),$$ and from this that $$\int x^k\,dx = \frac{x^{k+1}}{k+1} + C.$$
