Are they all similar to each other?

Question

I have a confusion. I have read one statement."It can be shown that the Jordan normal form of a given matrix A is unique up to the order of the Jordan blocks"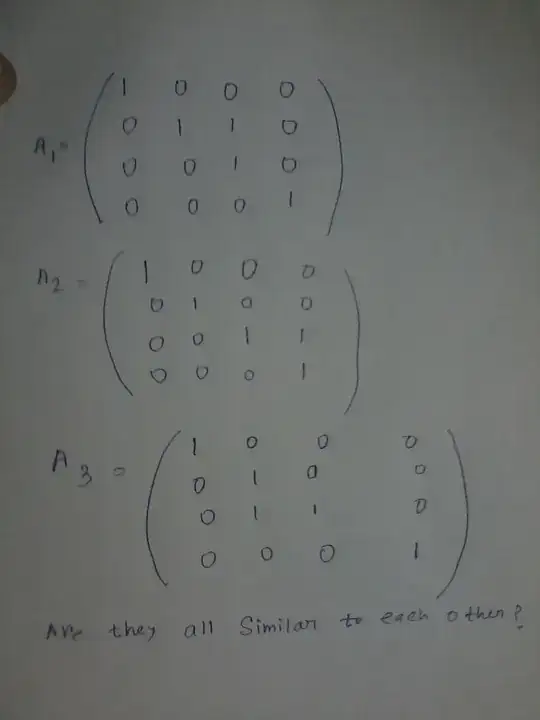. But I could not understand. I have taken an exercise. If this is solved I think my confusion will go away.

Note that $A_3=A_1^T$. Hence they are similar - see this duplicate. Now try to find out why $A_2$ is similar to it, too. — Dietrich Burde, Aug 05 '17 at 18:05
If u ignore this then would $A_3$ be still similar to $A_1$? — , Aug 05 '17 at 18:07
Yes, $A_1$ then would still be similar to $A_3$. It is really similar to $A_3$, take a permutation matrix $S$ with $A_1=SA_3S^{-1}$. — Dietrich Burde, Aug 05 '17 at 18:07
okk I got it.. Can u tell me how $A_1$ and $A_2$ are similar to each other?@DietrichBurde — , Aug 06 '17 at 00:46

score 0 · Accepted Answer · answered Aug 06 '17 at 08:15

Yes, they are all similar. Because the transpose of $A_1$ is $A_3$, these two matrices are similar, because $A$ and $A^T$ are always similar (see this duplicate). To see that $A_1$ and $A_2$ are similar, we just can find an invertible matrix $S$ such that $A_1S=SA_2$, which means to solve a system of linear equations in the coefficients of $S$. This may not be the most elegant way, but it certainly helps to find the answer. We obtain as one of many possible solutions $$ S=\begin{pmatrix} -1 & 1 & 0 & 0 \cr 1 & 0 & -1 & 0 \cr 0 & 0 & 0 & -1\cr 1 & 0 & 0 & 0\end{pmatrix}. $$ Indeed, $A_2=S^{-1}A_1S$.

score 0 · Answer 2 · answered Aug 06 '17 at 11:40

Not a complete answer, but too much for a comment:

If you have a block diagonal matrix $$ J= \begin{pmatrix} J_1 & & & & & 0 \\ & \ddots & & & & \\ & & J_k & & & \\ & & & J_{k+1} & & \\ & & & & \ddots & \\ 0 & & & & & J_m \end{pmatrix} $$ you can swap the blocks $J_k$ and $J_{k+1}$ using the following change of basis matrix $$ S=\begin{pmatrix} I_1 & & & & & 0 \\ & \ddots & & & & \\ & & \mathbf{0} & I_k & & \\ & & I_{k+1} & \mathbf{0} & & \\ & & & & \ddots & \\ 0 & & & & & I_m \end{pmatrix} $$ where $I_i$ is the identity matrix of the same size as the matrix $J_i$ for all $i\in\{1,\ldots,m\}.$ $$ S^{-1}JS = \begin{pmatrix} J_1 & & & & & 0 \\ & \ddots & & & & \\ & & J_{k+1} & & & \\ & & & J_k & & \\ & & & & \ddots & \\ 0 & & & & & J_m \end{pmatrix} $$ This shows that you can obtain each possible arrangement of Jordan blocks with similarity transformations, because each possible reordering of the diagonal blocks can be obtained by swapping adjacent diagonal blocks.

Are they all similar to each other?

2 Answers2