12

Penrose's paper On the cohomology of impossible figures suggests me that we can't draw such an impossible figure on a contractible part $Q$ of a sheet of paper so that it completely fills it, because the first cohomology group $H^1(Q,G)$ of such a domain is trivial (where G is the ambiguity group of the figure) (see also here) 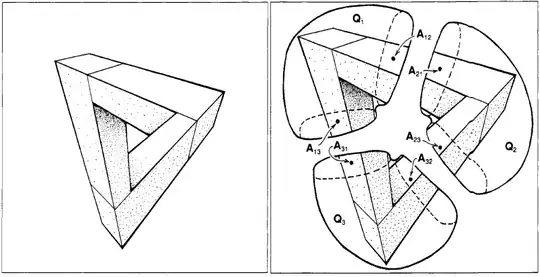penrose tribar Still he does some, e.g. this (the picture is taken from here):

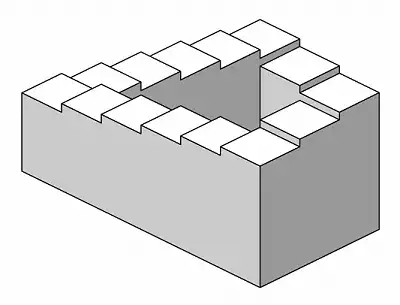
impossible staircase

Why is it possible? And what is the general, true relationship between the impossibility of figures and cohomology? Cohomology of what, if not of the drawing domain?

Edit

I try to make my problem a bit clearer.

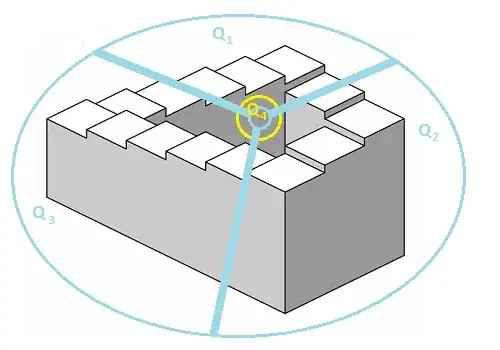
Here is a good cover of the solid disk on the paper containing the picture of the impossible staircase.

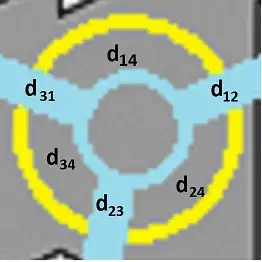
enter image description here

$Q_1$, $Q_2$ and $Q_3$ correspond to the open sets of Penrose (their overlapping areas are the thick radial blue lines), while $Q_4$, the solid disk bounded by the yellow circle, is an additional open set that overlaps with each other $Q$-s. I show the middle of the figure in big:

enter image description here

Here $d_{ij}$ stands for the same as in Penrose's paper. I think, that we have some problem with $d_{14}$, $d_{24}$ and $d_{34}$, but I don't know, what.

mma
  • 2,033

2 Answers2

11

The drawing domain of most impossible figures is a circle or an annulus. The reason they're impossible is that there is no single "height function" that covers all of it, even though there is a "steepness function".

In other words, there exists a function that looks like it should be a derivative / gradient, but isn't. That's exactly what non-trivial cohomology is all about. This is impossible on a simply connected domain like the whole plane or a solid disc, but it is very much possible on a circle / annulus.

Arthur
  • 199,419
  • The second exaple (the impossible staircase) is drawn on simply connected domain. And just this is the point of my question. – mma Aug 04 '17 at 05:16
  • 2
    No, the stairs themselves cover a circle. Whatever they choose to colour the background, it is the steps themselves, not the solid block below them which is impossible. It's just there for the psychological effect, making sure you think of them as stairs (and therefore attribute a steepness to it) and not just a squiggly line. – Arthur Aug 04 '17 at 05:18
  • Yes, but then cohomology of what is that we talk about? Of the space where the real object is located? This is meaningless in the case of an impossible object, isn't it? – mma Aug 04 '17 at 05:22
  • 2
    The area of paper that the impossible figure occupies is what we're talking about. The non-trivial cohomology guarantees that you can't "fill in the void" in the middle of the figure on the paper in any way that respects the steepness it already has, but if the figure was really lying in three-dimensional space, then we could've lain planks across it. Thus the non-trivial cohomology of the two-dimensional drawing shows it cannot be situated in three-dimensional space as we know it, and therefore is impossible. – Arthur Aug 04 '17 at 05:28
  • 2
    @mma It has been a long time since I fiddled with this, but I think the what's happening is the following: even if your object is impossible, you can cover it by open sets which are individually possible, modulo gluing information of those "possible pieces". One is taking the Cech cohomology of that data to see that it is not realizable as a possible configuration, on the whole. – Balarka Sen Aug 04 '17 at 05:32
0

I think, I misunderstood the role of the annulus. My conclusion is that we can draw an impossible figure on any domain of a sheet. The annulus (or any non-contractible open set) is not a constraint. It is only a tool for testing the possibility of the picture. The test is that the cocycle $d_{ij}$ described in Penrose's paper is a coboundary, or not. That is, the true relationship between cohomology and the impossible figures is simply the following.

A locally realistic figure is globally impossible if and only if there is a non-contractible open subset of the drawing domain on which the cocycle $\{d_{ij}\}$ is not a coboundary.

mma
  • 2,033