$$\int_{0}^{+\infty} \frac{\sin(x)}{x} e^{itx} dx = ?$$
I know the Laplace transform of sinc is $\arctan(1/t)$. However, what if $t$ is a complex number?
Asked
Active
Viewed 331 times
3
-
Hehe, I bet MV would like to write $\sin(x)=\frac{e^{ix}-e^{-ix}}{2i}$ and apply the generalized Frullani theorem. – Simply Beautiful Art Aug 02 '17 at 15:53
-
@SimplyBeautifulArt Your guess is correct ... ;-) – Mark Viola Aug 02 '17 at 16:06
3 Answers
2
Note for $\text{Im}(t)\ge 0$ we have
$$\int_{-\infty}^\infty \frac{\sin(x)}{x}\,e^{itx}\,dx=\frac1{i2}\int_{-\infty}^\infty \frac{e^{i(t+1)x}-e^{i(t-1)}x}{x}\,dx$$
Applying the Complex Version of Frullani's Integral yields
$$\begin{align} \int_{-\infty}^\infty \frac{\sin(x)}{x}\,e^{itx}\,dx&=\frac1{i2}\int_{0}^\infty \frac{e^{i(t+1)x}-e^{i(t-1)}x}{x}\,dx\\\\ &=\frac{1}{i2}\log\left|\frac{t+1}{t-1}\right|+\frac12\left(\arctan\left(\frac{\text{Re}(t)+1}{\text{Im}(t)}\right)-\arctan\left(\frac{\text{Re}(t)-1}{\text{Im}(t)}\right)\right) \end{align}$$
Mark Viola
- 179,405
-
-
-
Saw you edit the question, and instinct just said that this is what you'd do, since you were probably planning to write up an answer ;) – Simply Beautiful Art Aug 02 '17 at 16:08
-
Is it obvious the last term reduces to $C 1_{|t| < 1}$ when $t$ is real ? It could depend on the branch I'd say. – reuns Aug 02 '17 at 16:22
1
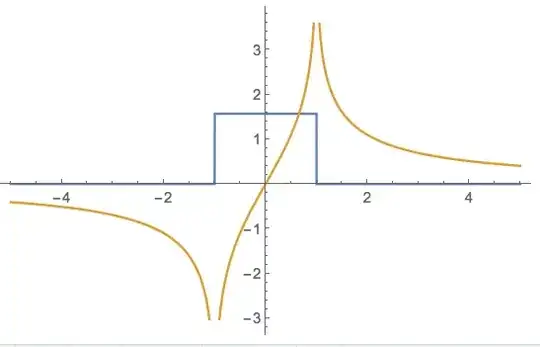
In term of distributions, the Fourier transform of $\frac{\sin(\pi x)}{\pi x}$ is $1_{|\xi| < 1/2}$ and the FT of $1_{x > 0}$ is $\frac{1}{2i \pi}\frac{d}{d\xi} \log |\xi| + \frac{1}{2} \delta(\xi) $,
thus the FT of $\frac{\sin(\pi x)}{\pi x}1_{x > 0}$ is $$1_{|\xi| < 1/2} \ast (\frac{1}{2i \pi}\frac{d}{d\xi} \log |\xi| + \frac{1}{2} \delta(\xi)) = \frac{\log|\xi + 1/2| - \log|\xi - 1/2| }{2i \pi}+ \frac{1_{|\xi| < 1/2} }{2}$$
reuns
- 77,999
-
Just curious ... how is the Dirac Delta defined on $\mathbb{C}$? That is, how does one define the distribution $\delta(\xi)$? – Mark Viola Aug 02 '17 at 19:01
-
@MarkViola You don't in general. But if you really want to, say when considering the analytic continuation of (inverse) Laplace transforms, you can define an analytic functional $\delta(z-a)= \lim_{N \to \infty}\int_{\sigma-iN}^{\sigma+iN} e^{-s(z-a)}ds$ the limit being in the sense of distributions on a space of analytic test functions. In this framework, the Laplace/Fourier transform of $e^x$ could be $\delta(z-i)$. – reuns Aug 02 '17 at 19:06
-
So, was it in that spirit that you wrote $\delta(\xi)$? I'm asking since the OP specified an interest in complex values of $t$, where $t$ was the transform variable (i.e., the OP's $t$ is your $\xi$ I beleive). – Mark Viola Aug 02 '17 at 19:11
-
@MarkViola Right, I answered to the title, the Fourier transform. Also for $\Im(t) > 0$ instead of Frullani theorem you can integrate $\int_0^\infty \sin(x) e^{-sx}dx$, which is what suggests what he wrote about $\arctan$ ? – reuns Aug 02 '17 at 20:01
-
If you want to adapt my answer, then the FT of $e^{-\sigma x}1_{x > 0}$ is $\frac{1}{\sigma+2i \pi \xi}$ and the result (up to $\omega = 2i \pi \xi$) is $1_{|\xi| < 1/2} \ast \frac{1}{\sigma+2i \pi \xi} = \arctan \ldots$. So I still think the term $\frac{1_{|\xi| < 1/2}}{2}$ appears from the branch of $\arctan$ – reuns Aug 02 '17 at 20:04
0
$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,}
\newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace}
\newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack}
\newcommand{\dd}{\mathrm{d}}
\newcommand{\ds}[1]{\displaystyle{#1}}
\newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,}
\newcommand{\ic}{\mathrm{i}}
\newcommand{\mc}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\pars}[1]{\left(\,{#1}\,\right)}
\newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}}
\newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,}
\newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}}
\newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$
\begin{align}
&\int_{0}^{\infty}{\sin\pars{x} \over x}\,\expo{\ic tx}\,\dd x =
\int_{-\infty}^{\infty}\bracks{x > 0}{\sin\pars{x} \over x}\,\expo{\ic tx}
\,\dd x
\\[5mm] = &\
\int_{-\infty}^{\infty}\bracks{\int_{-\infty}^{\infty}{\expo{\ic kx} \over
k - \ic 0^{+}}\,{\dd k \over 2\pi\ic}}
{\sin\pars{x} \over x}\,\expo{\ic tx}\,\dd x =
\int_{-\infty}^{\infty}{1 \over k - \ic 0^{+}}\int_{-\infty}^{\infty}
{\sin\pars{x} \over x}\,\expo{\ic\pars{k + t}x}\,\dd x\,{\dd k \over 2\pi\ic}
\\[5mm] = &\
\int_{-\infty}^{\infty}{1 \over k - \ic 0^{+}}\int_{-\infty}^{\infty}
\pars{{1 \over 2}\int_{-1}^{1}\expo{-\ic qx}\,\dd q}
\,\expo{\ic\pars{k + t}x}\,\dd x\,{\dd k \over 2\pi\ic}
\\[5mm] = &\
{1 \over 2}\int_{-\infty}^{\infty}{1 \over k - \ic 0^{+}}\int_{-1}^{1}
\int_{-\infty}^{\infty}
\expo{\ic\pars{k + t - q}x}\,\dd x\,\dd q\,{\dd k \over 2\pi\ic}
=
{1 \over 2}\int_{-\infty}^{\infty}{1 \over k - \ic 0^{+}}\int_{-1}^{1}
2\pi\,\delta\pars{k + t - q}\,\dd q\,{\dd k \over 2\pi\ic}
\\[5mm] = &\
{1 \over 2\ic}\int_{-\infty}^{\infty}
{\bracks{-1 < k + t < 1} \over k - \ic 0^{+}}\,\dd k =
{1 \over 2\ic}\int_{-1 - t}^{1 - t}{\dd k \over k - \ic 0^{+}}
\\[5mm] = &\
{1 \over 2\ic}\,\mrm{P.V.}\int_{-1 - t}^{1 - t}{\dd k \over k} +
{1 \over 2\ic}\,\ic\pi\bracks{-1 - t < 0 < 1 - t}
\\[5mm] & =
-\,{\ic \over 2}\left\{%
\bracks{1 - t < 0}\ln\pars{t - 1 \over t + 1} +
\bracks{-1 - t < 0}\bracks{1 - t > 0}\ln\pars{1 - t \over 1 + t}\right.
\\ &\
\left.\phantom{-\,{\ic \over 2}\left\{\right.} +
\bracks{-1 - t > 0}\ln\pars{1 - t \over - 1 - t}\right\} +
{\pi \over 2}\,\bracks{-1 < t < 1}
\\[5mm] & =
-\,{\ic \over 2}\left\{%
\bracks{t > 1}\ln\pars{t - 1 \over t + 1} +
\bracks{\verts{t} < 1}\ln\pars{1 - t \over 1 + t}\right.
\\ &\
\left.\phantom{-\,{\ic \over 2}\left\{\right.} +
\bracks{t < - 1}\ln\pars{1 - t \over - 1 - t}\right\} +
{\pi \over 2}\,\bracks{-1 < t < 1}
\\[5mm] = &\
\bbx{\bracks{\vphantom{\Large A}\verts{t} < 1}{\pi \over 2} +
{1 \over 2}\bracks{\vphantom{\Large A}\verts{t} \not= 1}
\ln\pars{\verts{t + 1 \over t - 1}}\,\ic}
\end{align}
Felix Marin
- 89,464