3

Math gurus...

I am looking for a way to tell if a line passes through a triangle as shown in the diagram below - the line described by the points p0 and p1 pass through the triangle described by the vertices v0, v1, v2:

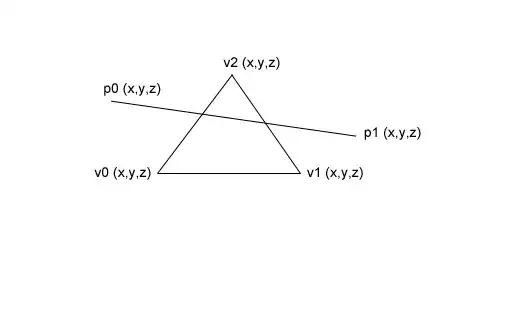
enter image description here

I will readily admit, I don't have a clue -- so any help is appreciated as always!

gue
  • 328
bdcoder
  • 145
  • 2
    You can evaluate the points $v_1,v_2,v_3$ on $f(x,y)=ax_by_c$, where $ax+by+c=0$ is the equation of the line. If there is at least one change of sign (the values of $f$ are some negative and some positive) then True, else False. – Peyton Aug 01 '17 at 02:16
  • 3
    @Peyton: Please post an answer! See this for some reasons why: https://math.meta.stackexchange.com/questions/1559/dealing-with-answers-in-comments – Aryabhata Aug 01 '17 at 02:20
  • Thanks guys -- its a start... and I'll do my part, but I do not have a Phd in computational-geometry, so if someone wants to show step by step calculations for a complete newbie such as myself, that would be great - as the mathematical notation (which is English to you) is greek to me!! -- but I still appreciate those that can at least kick me in the right direction ! – bdcoder Aug 01 '17 at 02:31
  • If $p_1=(x_1,y_1)$ and $p_2=(x_2,y_2)$, then the equation of the line is $(x_2-x_1)(Y-y_1)-(y_2-y_1)(X-x_1)=0$. We only care about the expression on the left-hand side. Assume that $v_1=(a_1,a_2)$, $v_2=(b_1,b_2)$, and $v_3=(c_1,c_2)$. Then plug $a_1$ where $X$ is and $a_2$ where $Y$ is. Record the sign. Do the same for $v_2, v_3$. If the results contained positive and negative values, then the line passed through the interior of the triangle. If there was a $0$ and all others were of the same sign, it passes through a vertex. – Peyton Aug 01 '17 at 02:38
  • You appear to be working in 3-D. Question 1: are you really? Question 2: If so, are all of the points known to be coplanar, or do you have an arbitrary triangle and line segment? – amd Aug 01 '17 at 06:41
  • @Peyton , why not write your comments up as an answer? – G Tony Jacobs Aug 01 '17 at 12:48
  • @amd - yes, the points are coplanar - the data I am using includes x, y and z coordinates – bdcoder Aug 02 '17 at 00:14
  • In that case, you’ll need to take some care if you’re going to be coding up the mathematical solutions you’re likely to get here. Small perturbations to the data can disrupt the coplanarity and lead to false results. – amd Aug 02 '17 at 00:19
  • One other question: are you interested in the line segment, as illustrated, or in the entire line through $p_0$ and $p_1$? – amd Aug 02 '17 at 00:28
  • @amd just the line segment as illustrated; that is, if ANY part of the line passes through I just need to know -- also, Peytons solution works when using (x,y), but my data has (x,y,z); because the points are coplanar can I simply drop one of the coordinates? – bdcoder Aug 02 '17 at 01:22
  • That should work, and is not particularly sensitive to data inaccuracies. Essentially, you’re projecting everything onto one of the coordinate planes, which preserves incidence relationships. Be careful not to collapse the triangle, which can happen if it’s parallel to the axis you decide to drop. Note, though, that @Peyton’s solution is for the entire line, not a segment of it. – amd Aug 02 '17 at 01:32
  • Line or line segment ? Are the points really 3D ? –  Aug 02 '17 at 06:26
  • Apply a transformation that moves the vertices of the triangle to $(0,0,0)$, $(1, 0, 0)$ and $(0,1,0)$. Then your problem becomes a matter of deciding whether the transformed segment has a point whose $x$ and $y$ coordinates are positive (well, non-negative, if you allow points on an edge) and have a sum smaller than (or, perhaps, not greater than) $1$. There could be a clever way to check this; I haven't looked that hard. That said, the coordinate transformation will almost-always introduce computational error. Ideally, a strategy for the simple case would be back-transformed for the general. – Blue Aug 02 '17 at 06:32

2 Answers2

3

The triangle $\Delta(v_0,v_1,v_2)$ defines a plane $\Pi$. If the line $\ell$ is not parallel to $\Pi$ it will intersect the plane in exactly one point $p$. Then we can apply three determinants $det(p,v_0,v_1)$, $det(p,v_1,v_2)$, and $det(p,v_2,v_0)$ determine the orientation (sign) and know if $p$ lies inside of $\Delta$, if so then $\ell$ intersects $\Delta$.

To calculate $p$ we can use the parametric form (Wikipedia):

$\Pi$: $v_0 + (v_1 - v_0)u + (v_2-v_0)w$

Assuming $\ell$ is defined by two points $p_0$ and $p_1$. Then we can write the point of intersection as:

$p_0 + (p_1-p_0)t = v_0 + (v_1 - v_0)u + (v_2-v_0)w$

$\Leftrightarrow p_0 - v_0 = (p_0 - p_1)t + (v_1 - v_0)u + (v_2-v_0)w$

Three equations (one for each $x$, $y$, and $z$) three unknown variables ($t$, $u$, and $w$) gives us an exact solution.

Then $p$ lies in the plane $\Pi$ and we can see the problem as $2D$ point location problem where we have to find out if $p$ lies inside of $\Delta$. Here we apply the three determines as explained above.

EDIT: Coplanarity was given later and only in the comments.

In case all points a coplanar we can simply calculate $det(p_0,p_1,v_0)$, $det(p_0,p_1,v_1)$, and $det(p_0,p_1,v_2)$. If one sign is different the line passes trough $\Delta$ otherwise it does not. (This variant was already described by another answer but as it seems it was deleted.)

gue
  • 328
  • Thanks, I adapted the answer. – gue Aug 02 '17 at 06:23
  • Thank-you very much for your answer (coplanar points), I ran several tests and everything seems to work. In the case where the intersection contains an edge of the triangle, it seems two of the determinants will be zero -- is that correct? I tested 5 scenarios: 1 - No intersection, 2 - Intersection at vertex, 3 - Intersection through 2 edges, 4 - Intersection contains edge, 5 - Intersection through 1 vertex and edge. – bdcoder Aug 03 '17 at 03:28
  • Yes that is correct. (The $det()$ gives the signed area (volume) which is zero in that case.) I think that are all cases that you need. – gue Aug 03 '17 at 05:30
  • while testing the case of the line through a vertex and an edge, the results contain positive, negative and a zero value. Is this another case in addition to what Peyton mentioned, ie: "If there was a 0 and all others were of the same sign, it passes through a vertex"? Looking to build a truth table with regard to the returned results (positive, negative and zero values) in order to build the logic that returns true if the line passes through the triangle or not. – bdcoder Aug 03 '17 at 16:38
  • If all determinants are strictly larger zero there is no intersection. The same for strictly smaller than zero. Otherwise, an intersection exists. Do you need to know an intersection type? – gue Aug 03 '17 at 16:52
  • no, I only need to know if the line passes through the triangle (2 edges) or passes through a vertex or side (hope that makes sense), basically the 5 cases I mentioned above. – bdcoder Aug 03 '17 at 17:00
  • I just realized while doing more testing that if I have a vertical line segment BELOW the base of the triangle the determinants are (>0), (<0),(>0), which would indicate an intersection (but there is none), so I am hooped again! -- and it is probably my own doing because I did not ask to differentiate between a line and a line segment? I may need to re-post the problem. – bdcoder Aug 04 '17 at 03:00
0

Ingredients:

1) Equation of a plane determined by three points in the space.

2) Parametric equation of the line T passing through $p_0,p_1$, and of the three lines bordure of the triangle.

3) Put line T coordinates obtained in the plane equation.

4)Put you triangle inside a parallepipede L $(x_{min},x_{max})\times (y_{min},y_{max})$

The line passes through the plane if in 3) we get equation verified for any point of T.

The line T intersectes the triangle if the point of intersections of T with line bordures when they exist are in L.

Toni Mhax
  • 1,252