8

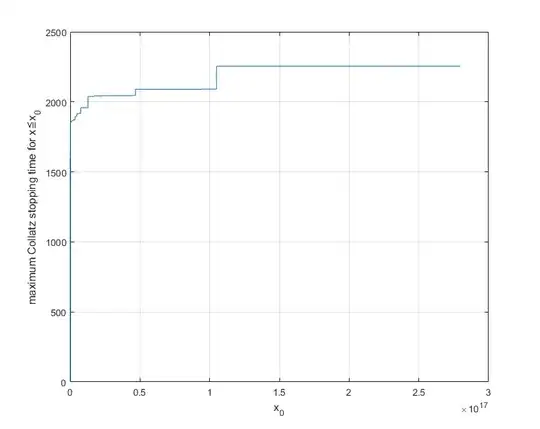
The maximum stopping times for the Collatz $3x+1$ function have been computed up to about $x = 10^{18}$, given at $3x+1$ delay records. Plotting those results gives this:

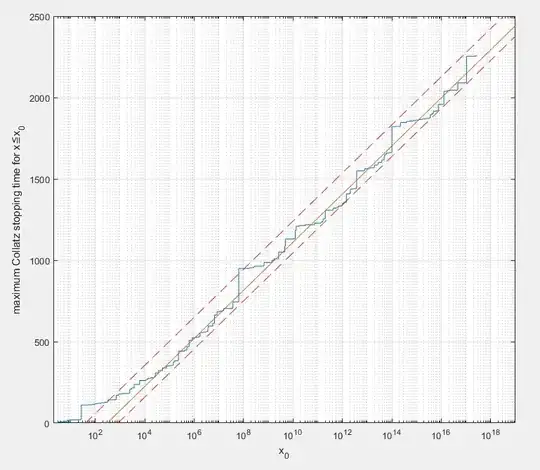
enter image description here

A more interesting presentation is given on a semi-log plot:

enter image description here

It can be seen that the stopping time tends to a line as $x$ increases, and is confined to relatively narrow bounds. If anything, it seems to be tending to slightly narrower bounds as $x$ increases. Using a best fit of the upper part of the curve gives this equation:

$S=147.8\log_{10}x-366.9$

where $S$ is the maximum stopping time.

My question is, is there a (perhaps statistical) argument for why the maximum stopping time would tend to follow this line?

A further question is what is the likelihood that the relation could hold at higher powers of 10. For example, $x_0=10^{200}$ gives a predicted maximum stopping time for $x<x_0$ of about 29,194.

Joe Knapp
  • 1,170
  • Just about terminology: WP says "stopping time" is the number of iterations until $a_n \lt a_1$, then "delay" by Eric Roosendaal is the number of iterations until $a_n=1$, and this is sometimes used as "total stopping time" because "stopping time" alone seems to have been introduced by Riho Terras already in 1976. And in so wide use after that that it became somehow standard with that meaning. Because you use the "delay"-table of Roosendaal, I suspect you mean "total stopping time" instead of "stopping time"? – Gottfried Helms May 01 '21 at 09:23

1 Answers1

1

I can't really explain it exactly but I can give a heuristic to see that this is basically the simplest scaling that makes any sense.

Suppose $x$ is a number whose Collatz iteration reaches the familiar cycle $4 \to 2 \to 1 \to 4 \to \dots$ Then there is a number $S_x$, the number of iterates before reaching $1$, and a number $p_x$, which is the fraction of its iterates that are even (again counting only until the first time that the sequence reaches 1). For example, $S_5=5,p_5=4/5$. An even Collatz iterate gives a division by 2 and an odd Collatz iterate roughly gives a multiplication by 3, so the Collatz sequence should be just a little bit bigger than $x_n=x 2^{-np_x} 3^{n(1-p_x)}=x 3^n 6^{-np_x}=x (3 \cdot 6^{-p_x})^n$ (bigger because I've dropped the $+1$s). If $p_x>\log(3)/\log(6)$ which is between $0.61$ and $0.62$ then this goes exponentially to zero.

The statement $S_x \sim k \log(x)$ for a constant $k$ amounts to saying that $p_x$ is asymptotically independent of $x$. If this holds then $S$ has the same asymptotic. Of course $p_x$ is actually a rather erratic function of $x$ in reality, but this is the main idea. Most likely this heuristic as stated is false but one could hope that something similar (for example, a relation involving aggregate statistics like your $S$) might hold.

Ian
  • 101,645
  • Thanks, Ian. Empirically, $p_x$ does seem to clock in very near 0.5 for large $x$, so your conclusion would hold. For example, for $x=10^{200}$ $p_x$ is 0.5032, with a median stopping time of 3275. – Joe Knapp Jul 31 '17 at 15:17
  • @JoeKnapp $p_x$ should actually clock in above $0.6$ for any Collatz sequence that reaches the 4,2,1 cycle. – Ian Jul 31 '17 at 15:22
  • Lagarias in "The 3x+1" problem notes: "probabilistic models for the $3x+1$ function iteration predict that even and odd iterates will initially occur with equal frequency.."

    That seems to be borne out by just trying numbers, such as $x^{200}$ above.

     – Joe Knapp Jul 31 '17 at 15:29
  • @JoeKnapp I'm not sure I follow. I'm talking about the usual Collatz iteration: even numbers are divided by $2$, odd numbers are multiplied by $3$ and then $1$ is added. To reach $1$ under this iteration you must necessarily encounter more even iterates than odd iterates because the effect of each division is smaller than the effect of each multiplication. I think you may be referring to some simpler system, such as just measuring the parity of a pure 3x+1 iteration. – Ian Jul 31 '17 at 15:30
  • PS One thing though: your heuristic applies to stopping time of a given starting value, but the statistic $S$ as defined above applies to the maximum stopping time observed for all values less than a given value. Maybe the same reasoning applies? There is a big difference in general between $S$ and the median or expected stopping time in a given region. – Joe Knapp Jul 31 '17 at 15:33
  • @JoeKnapp The heuristic thinks of the stopping time as being monotone. Of course it is not. But thank you, my notation in the answer was not consistent with yours. – Ian Jul 31 '17 at 15:35
  • Let us continue this discussion in chat. – Joe Knapp Jul 31 '17 at 15:43