6

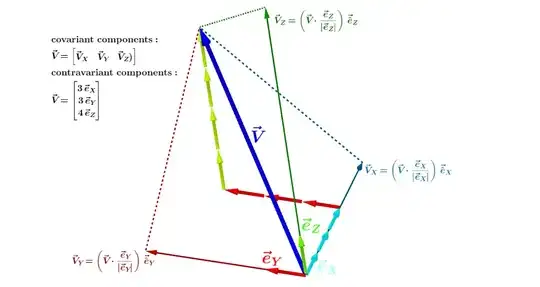
This youtube video by Eugene Khutoryansky makes the distinction clear between the covariant coordinates of a vector (dot product of the vector with each of the basis vectors or vector projection), and the contravariant coordinates (parallelogram law):

enter image description here

Is there a way you could explain to a lay person that this somehow underpins the following fact:

Covariant vectors are representable as row vectors. Contravariant vectors are representable as column vectors.

?

I would like to know, for example, if the idea carries beyond being able to calculate the length of a vector in non-Cartesian coordinates as the dot product of its covariant and contr$avariant expressions:

$$ \lVert V\rVert ^2=\begin{bmatrix} V_X & V_Y & V_Z\end{bmatrix}\cdot \begin{bmatrix} V^X \\ V^Y\\ V^Z\end{bmatrix}.$$

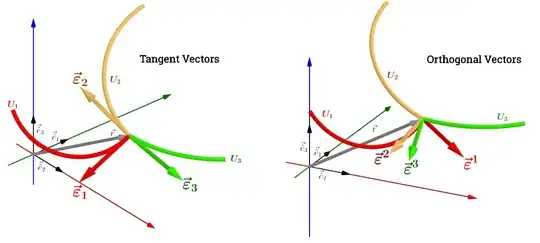
In a curvilinear system presumably the contravariant basis vectors would be tangential, whereas the covariant basis vectors would be orthogonal to the coordinates:

enter image description here

Apropos of the first comment, and if it can be confirmed (as a bonus), covariant vectors are covectors or dual vectors, while contravariant vectors are just vectors.

Antoni Parellada
  • 8,889
  • The last time someone used the words "covariant" or "contravariant" in my presence was around 1958. This might be an indication why you don't have received an answer so far. – Christian Blatter Jul 29 '17 at 09:21
  • 1
    Probably of interest: Dual space and covectors: force, work and energy. – Andrew D. Hwang Jul 29 '17 at 14:11
  • 3
    @ChristianBlatter You apparently stay clear of category theorists and physicists, then. – Bence Racskó Jul 29 '17 at 16:00
  • @Uldreth: Sorry. I didn't think of category theory, but of mathematical physics and differential geometry. – Christian Blatter Jul 29 '17 at 17:43
  • 1
    @ChristianBlatter Fair enough, now that you mention it, I am a physics student, but I have also only encountered these terms in textbooks and introductory tensor calculus courses as well, seems the physicists in the department themselves are not fond of it anymore.

    To be fair, I have read Ricci's original paper on tensor calculus and even there it wasn't clear why on Earth the vectors are the "contravariant" vectors and the dual vectors the "covariant ones", because by the logic of the paper it should be the other way around. Which is consistent with category theory too!

     – Bence Racskó Jul 29 '17 at 20:57

1 Answers1

3

You can represent "contravariant vectors" as rows and "covariant vectors" as columns all right if you want.

It's just a convention. The dual space of the space of column vectors can be naturally identified with the space of row vectors, because matrix multiplication can then correspond to the "pairing" between a "covariant vector" and a "contravariant vector".

Remember that "covariant vectors" are defined as scalar-valued linear maps on the space of "contravariant vectors", so if $\omega$ is a covariant vector and $v$ is a contravariant vector, then $\omega(v)$ is a real number that depends linearly on both $v$ and $\omega$. If you make $v$ correspond to a column vector, and make $\omega$ correspond to a row vector then $$ \omega(v)=\omega v=(\omega_1,...,\omega_n)\left(\begin{matrix}v^1 \\ \vdots \\ v^n\end{matrix}\right)=\omega_1v^1+...+\omega_nv^n. $$

If $\omega$ was the column instead, then the above matrix multiplication would look as $\omega(v)=v\omega$, which would not look as aesthetically pleasing, as we are used to displaying the argument of a function to the right of the function, and in this case $v$ is the argument.

Bence Racskó
  • 7,329
  • 25
  • 42
  • Thank you. This is very clear, and helpful. It would definitely clarify all the issues in the OP if you could touch on the geometry as sketched in the plot - I kind of see... at a very intuitive level that since the contravariant expression uses basis vectors tangent to the surface, while the covariant expression uses orthogonal projections, there ought to be a dot product lurking somewhere so as to keep the length of the vector independent of the coordinate system, or something along those lines... – Antoni Parellada Jul 29 '17 at 17:00
  • +1 for the index-convention and a commentary: if the $b_i$ is any basis for a vector space $V$, there's always a corresponding basis $\beta^j$ for $V^*$ such that $\beta^j(b_i)=\delta^j_i$. – janmarqz Jul 31 '17 at 18:58