2

Suppose we have two rationals, $\frac{a}b$ and $\frac{c}d$. I daresay anyone with some form of mathematical education would disagree that our result would be $\frac{a}b\times \frac{c}d=\frac{ac}{bd}$. That is, we multiply our numerators to get the result numerator and we multiply the denominator to get the result denominator. However, mathematically speaking, why do we do this?

If we consider the canonical definition of multiplication (i.e. repeated addition) in the case where we have two integers, say $3$ and $4$, we would come up with $(3\times 4) = (4 + 4 + 4)$. If this is so (and hopefully it is) what does it mean mathematically to add $\frac{c}d$ to itself $\frac{a}b$ times?

After doing a bit of research, all I've managed to come up with is this image. enter image description here

Unfortunately, I don't see how this has anything to do with multiplication and seems to me like little more than a tool for teaching grade schoolers.

This also led me to think about how we multiply decimal numbers. For example, $(0.2) \times (0.4) = 0.08$ (i.e. $2\times 4$ with the decimal moved over a number of places equal to the number significant digits past the decimal).

My intuition tells me that the answer to one of these will provide the answer to the other.

Lastly, excuse me if this question seems silly, but I've pondered it quite a bit and can't come up with anything mathematically rigerous.

EDIT: I changed all literal values to be arbitrary values (as they should have been originally).

EDIT 2: Please note that I am PERFECTLY CAPABLE of multiplying fractions together in any way shape or form. This is NOT a post about how to multiply fractions. This post is about fundamentally understanding what it means to multiply a pair of fractions together.

AldenB
  • 41
  • Think of multiplication as the area of a rectangle with the factors as side lengths. – Akiva Weinberger Jul 28 '17 at 14:45
  • @AkivaWeinberger Then we'd just be begging the question. The multiplication is necessary in order to find the area of a rectangle. – AldenB Jul 28 '17 at 14:50
  • Not necessarily. We know that a 1x1 rectangle has an area of 1. To find the area of a $\frac13\times\frac14$ rectangle, note that we can put twelve $\frac13\times\frac14$ rectangles together to make a $1\times1$ rectangle; hence, they must each have an area of $\frac1{12}$. – Akiva Weinberger Jul 28 '17 at 14:51
  • @AkivaWeinberger What about something like (19/41)*(17/97)? I think one would be hard-pressed to find the number of rectangles with those dimensions that could fit in the unit square without using conventional multiplication of fractions. – AldenB Jul 28 '17 at 14:57
  • 1
    @AldenB We want to prove that 3977 copies of that rectangle make a rectangle of area 323. That can be done quite easily. – Akiva Weinberger Jul 28 '17 at 15:00
  • 1
    @AldenB Alternatively, we can show using the previous method that each $\frac1{41}\times\frac1{97}$ rectangle has an area of $\frac1{3977}$, and note that 323 copies of that rectangle make one of size $\frac{19}{41}\times\frac{17}{97}$. Thus, it has area $\frac{323}{3977}$. – Akiva Weinberger Jul 28 '17 at 15:02
  • @Akiva XD But you only know that 1/41 * 1/97 = 1/3977 by using conventional multiplication of fractions methods! – AldenB Jul 28 '17 at 15:18
  • @AkivaWeinberger maybe I'm just horribly confused at this point. – AldenB Jul 28 '17 at 15:19
  • "But you only know that 1/41 * 1/97 = 1/3977 by using conventional multiplication of fractions methods!" - No, I said "using the previous method" — by which I mean, we can fit 3977 copies of a $\frac1{41}\times\frac1{97}$ rectangle into a $1\times1$ square, so it must have an area of $\frac1{3977}$. – Akiva Weinberger Jul 28 '17 at 16:37

4 Answers4

2

If this is so (and hopefully it is) what does it mean mathematically to add (1/4) to itself (1/3) times?

It means that whatever you get in the end, if you add it to itself 3 times, you'll get 1/4. So... Suppose $$\frac{1}{a} \cdot \frac{1}{b} = \frac{1}{c}$$ Then this is like saying that: $$\frac{1}{a} = \frac{1}{c} + \dots (b \text{ times}) \dots + \frac{1}{c}$$ which is $$\frac{1}{a} = \frac{b}{c}$$ then you can cross multiply (no division, here) and you'll get $c = ab$.

Kevin
  • 736
  • Allow me to make this more general, suppose we have (a/b)*(c/d)=(e/f). Then what do we do? (a/b)=(e/f) + ... ((d/c) times) ... + (e/f) still doesn't make sense. – AldenB Jul 28 '17 at 14:41
  • If you add (a/b) * (c/d) to itself d times, you'll get (a/b) * c: The main idea is that you can always "cancel" fractions (assuming an integer denominator) by adding to itself. – Kevin Jul 28 '17 at 14:45
  • Unless I'm misunderstanding, we're getting away from the question at hand at this point. I'm perfectly capable of solving these sorts of problems algebraically; I've been doing it for at least a decade. What I'm talking about here is a fundamental understanding of what it means to multiply a pair of fractions together. – AldenB Jul 28 '17 at 15:04
  • The problem is just this: The "canonical" definition of division is that it is the inverse of multiplication. So you can't get away from an algebraic explanation if you want a fundamentally rigorous answer. If you are looking for an intuitive answer (one amenable to grade schoolers), the picture you provided already does pretty well! – Kevin Jul 28 '17 at 15:10
  • Perhaps you're right. – AldenB Jul 28 '17 at 15:20
1

Let me stick to purely nonnegative counting numbers $\mathbb N^+ = \{1,2,3,\dots\}.$ One way that we do this mathematically rigorously is to define fractions as,

$\frac ab$ is the set of all pairs $(c, d)$ of these numbers in $\mathbb N^+$, such that $a\cdot d = b \cdot c.$

Note that on this account $\frac12$ and $\frac 24$ are equal because of set equality: two sets are equal when they contain exactly the same elements; these two sets contain exactly the same pairs.

Why does this definition get to the heart of fractions? Because if you think about what this definition says $\frac 13$ is, it says that it's a relation between numbers and their thirds. So the numbers in the set are $\{(1, 3), (2, 6), (3, 9), \dots \}$ and we are expressing that the first number is one third of the second number, for all whole numbers where we can easily decide these things.

We also see that we can get a lot of understanding about how these work just by looking at the element of the set with the smallest first element; we can go from $(1, 3)$ back to $\frac13$ pretty easily. This is of course reducing a fraction to its simplest terms by removing common factors from both sides. Let's quickly prove that this works. Suppose $a = n \cdot x$ and $b = n\cdot y$ for the common factor $n\ne 1.$ We want to show that $\frac ab$ and $\frac xy$ are the same sets. The direction of proving that if $(c, d)$ is in the set $\frac xy$ then it must be in the set $\frac ab$ is very easy: $x\cdot d = y\cdot c$ implies that $n\cdot(x\cdot d) = n\cdot(y\cdot c),$ apply the associative rule to find that $(n\cdot x)\cdot d = (n\cdot y)\cdot c$, and thus $(c, d)$ is in $\frac ab,$ too. However if you pay careful attention this logic is almost entirely reversible. The only tricky bit is to prove that in $\mathbb N^+$ if $n\cdot a = n \cdot b$ then $a=b,$ this is the only manipulation that can't obviously be performed "backwards" because division is not well-defined on $\mathbb N^+$. But this can be easily seen from the simpler fact that if $a < b$ then $n\cdot a < n\cdot b,$ by the repeated addition definition and the property of addition that if $a < b$ and $c < d$ then $a+c < b + d$. So therefore if $n\cdot a = n \cdot b$ it must be the case that $a \ge b$ but also, turning around the equals sign, that $b \ge a.$ The only way both of these can be true is if $a=b.$

Addition of fractions

Now we also have an embedding of the numbers $\mathbb N^+$ in the fractions, that is as these fractions $\frac n1 = \{(n, 1), (2n, 2), (3n, 3), \dots \}.$ We look at the smallest elements and we see that when we add them we must perform $(n_1, 1) + (n_2, 1) = (n_1 + n_2, 1).$ The problem is, how do we make this well-defined so that it doesn't matter which pair we choose? Clearly if we chose $(2n_1, 2) + (3 n_2, 3)$ we would have to get $(k(n_1 + n_2), k)$ for some $k$. And the most obvious way to get this property is to say that $k=2\cdot 3$ so that we get $6(n_1 + n_2)$ for that first term, which we can do by multiplying the first item of the first term with the second item of the second term and the second item of the first term with the first item of the second term, so we have to generalize $(a, b) + (c, d) = (ad + bc, bd)$ to fully account for addition of the "natural number subset" of the rational numbers, in the case where we pick a representative element which isn't the smallest element.

Well then we are just stuck asking, "how do we extend this to non-natural numbers?" and the obvious answer is, just the most obvious way! Define that $\frac ab + \frac cd = \frac{ad+bc}{bd},$ and we get a valid expression for everything, which is the correct expression for the naturals. The proof that this is well-defined is simply that $\frac ab + \frac{nc}{nd} = \frac{n(ad+bc)}{n(bd)},$ so "by construction" this plays nice with our ability to reduce a fraction to lowest terms.

Exercise: also prove that this preserves the associative and commutative properties of addition.

Multiplication as repeated addition on the fractions

Something similar happens when we want to multiply with this new formula. Suppose we want to multiply $\frac 25$ by repeatedly adding it to itself 3 times, we find that the above expression gives first $\frac25 + \frac25 = \frac {20}{25}$ and then $\frac 25 + \frac {20}{25} = \frac{50+100}{125}.$ What do we notice? The bottom-most number is clearly $5\cdot 5 \cdot 5 = 5^3,$ the multiplication by $3$ cubes this denominator.

The top-most number is also growing, though, because we had $5 \cdot 2 + 5 \cdot 2$ and then this became $5^2\cdot 2 + 5\cdot(5\cdot 2) + 5\cdot (5\cdot 2)$ and we see that we got $5^2\cdot(2+2+2).$ Trying $4\cdot$ as repetition we find the pattern $5^3\cdot(2+2+2+2)/5^4.$ It's not hard to prove that adding $\frac ab$ to itself $n$ times produces $\frac{na}{b}.$

But what did we do last time we wanted to generalize addition to fractions? We considered the other representations of the integers. We know that we need $(p~n, p) \cdot (q~a, q~b)$ to produce $(r~n~a, r~b)$ because that is the self-addition pattern for integers. The obvious choice is $r=p~q$ which we can get by multiplying the first two and then multiplying the second two.

This suggests a product rule as $\frac ab \cdot \frac cd = \frac{ac}{bd}.$ Again we can immediately see that it's well defined with respect to simplifying to lowest terms, it's even more obviously associative and commutative than addition was.

But what really makes this multiplication is the distributive rule. Recall the distributive rule: $a\cdot(b + c)$ needs to be exactly the same value as $a\cdot b + a \cdot c$ and vice versa. If these two new definitions for addition and multiplication do not "play nice together" then we will need to fix one or the other!

Well, long story short, they do. We find that $$\frac ab\cdot\left(\frac cd + \frac ef\right) = \frac ab\cdot \frac{cf+de}{df} = \frac{acf+ade}{bdf} = \frac{abcf+abde}{b^2df} = \frac{ac}{bd} + \frac{ae}{bf}. $$ Again, the logic is perfectly reversible and the surprise that these two guesses of "let's just do the simplest thing" yields this fundamental axiom of arithmetic again for the fractions, means that we were "really onto something here."

Now in what sense is $\frac13$ a repeated self-addition? Well, it's not quite! It's a "multiplicative inverse" which means it undoes a repeated self-addition. It's kind of like if we define $\mathbb N^+$ as repeated increment operations applied to a starting value $1$, when we get to negative numbers we must have repeated decrement operations that undo the repeated increment. So $2$ represents "increment twice," then $-2$ must represent "decrement twice."

Similarly $\frac17 \cdot \frac ab$ is the number which, if you repeatedly add it to itself seven times, gives you $\frac ab$. It's the exact undoing of a repeated self-addition.

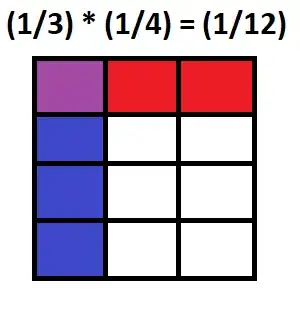
So when we do $\frac13 \cdot \frac14$ we are un-adding $\frac14$ from itself 3 times, meaning that we're trying to find the number which when added to itself 3 times would give $\frac14$. This is precisely just $\frac1{12}.$

CR Drost
  • 2,912
0

note that integers a and b can be rewritten as ${a\over 1}$ and ${b\over1}$ this has to equal ab=12 to stay consistent. The simplest way to do that, is to say lets make it a rule that we multiply numerators and denominators separately and combine the results so we have $ab=12\implies {ab\over1(1)}={ab\over1}=ab=12$ the rule when followed for other fractions produces the given results.

0

One could make use the fact that $\Bbb R$ is a field and use the field axioms (http://mathworld.wolfram.com/FieldAxioms.html) to prove these equalities rigorously.

For instance we could make use of the distributive property of $\Bbb R$ as follows, $$3\times4=3\times(1+1+1+1)=3+3+3+3=12$$

Next, $(1/a)$ is nothing but the inverse of $a$ $(a\neq0)$. So,

$$(1/3)\times(1/4)=3^{-1}\times4^{-1}=(3\times4)^{-1}=12^{-1}=(1/12)$$

Basically all the calculations stand on the shoulders of the Axioms.

Naive
  • 1,762
  • The important step here is $3^{-1}\times4^{-1}=(3\times4)^{-1}$, which should be proved. – Akiva Weinberger Jul 28 '17 at 14:52
  • @AkivaWeinberger That's true. But one can prove it from the fact that "a field is a commutative ring with unity" – Naive Jul 28 '17 at 15:03
  • And the proof is that $(4\times3)\times(3^{-1}\times4^{-1})={}$$(3^{-1}\times4^{-1})\times(4\times3)=1$ through the associative property, so $3^{-1}\times4^{-1}=(4\times3)^{-1}$. (And we may or may not want to point out how to prove that inverses are unique.) Right? – Akiva Weinberger Jul 28 '17 at 15:05
  • It's probably a good idea to explicitly list the field axioms in your answer (or at least link to them), by the way – Akiva Weinberger Jul 28 '17 at 15:07
  • @AkivaWeinberger Well again if at all one is so particular about the uniqueness of the inverses, we will have to prove that too! – Naive Jul 28 '17 at 15:11
  • @AkivaWeinberger I've included a link to the Field Axioms in my answer. – Naive Jul 28 '17 at 15:14
  • That proof is simple as well, right? If $x$ and $y$ are both inverses of $a$, then $x=x(ay)=(xa)y=y$. – Akiva Weinberger Jul 28 '17 at 16:39