16

This question is related to my bath towel, which I hang on a rope, so let's have fun (you can use your own towel to do this experiment in bath-o).

There is this rectangle with sides $a<b$. The rectangle is bent along a line that passes through the center of the rectangle. At which angle $\alpha$ (i. e., angle $\angle RAU$ – see the picture) should we bend the rectangle in order to get the minimum area of crossing intersection?

It is obvious that if $|a-b| \gg 0$, then $\alpha\approx\pi/4$. Also, we can look at the pentagon NOPQR. In addition to that, for a certain $a/b$ we get the triangle ($a/b<0.8150237, \alpha =\pi/4$).

All in all, I am looking for a graph: $a/b$ as in terms of $\alpha$ and the area of the crossing intersection, which is $\displaystyle S = [2ab - (a^2+b^2)t + 2abt^2 - (a^2+b^2)t^3]/[4(1-t^2)]$, where $t=\tan \alpha$.

Any help is highly welcome.

MAth towel

Mikhail G
  • 203
  • I assume alpha is the angle that the line through the center makes with one of the sides. Which side? – Matthew Conroy Feb 25 '11 at 19:14
  • The rectangle is bent along the line which goes through the diagonal crossing under alpha angle. ( I have a picture, but cannot upload it) – Mikhail G Feb 25 '11 at 19:29
  • Am I correct that you have given us the expression $S$ for the area as a function of $\alpha, a ,b$? All what you want to know is which value of $\alpha$ minimizes $S$ for a certain $b/a$? – Fabian Feb 26 '11 at 14:21
  • Yes, but please note that if $a<<b$, then you can bent $\pi/4$. If you have a=b, then I got: $\alpha=\pi/8$ What is beetween? – Mikhail G Feb 26 '11 at 19:17
  • You can set a=1 and measure in those units to get rid of one variable. Alpha will then take the derivative and set to zero, finding roots, but it is a mess – Ross Millikan Feb 26 '11 at 19:33
  • Ross, I bet that there will not be a mess at all! You should not use Ferrari's solution, but I really got stuck near critical bending. – Mikhail G Feb 26 '11 at 19:50
  • It looks like the optimal $\alpha$ is given by the roots of $t^4-4 t^2 + 8 [ab/(a^2+b^2)] t -1$. So how would you proceed without Ferrari? By the way the discriminant of this equation is zero for $a/b = \sqrt{29 - 6 \sqrt{6}} \approx 0.76$ which doesn't seem to agree with 0.81 you mentioned in the question... (I'm however not sure if it should) – Fabian Feb 26 '11 at 21:25
  • Look, S'=-(a^2+b^2)+8abt-4(a^2+b^2)t^2+(a^2+b^2)t^4=0. Let a/b=\tg \beta, then k=\sin 2\beta=2ab/(a^2+b^2), so t^4-4t^2+4kt-1=0, then imagine graphics: f=t^4-4t^2-1 and g=-4kt. Guess different k. Also, f=g, f'=g'--> C=k_0>5/(3\sqrt3), t_0=1/\sqrt3. C=2x/(1+x^2)--> T=(3\sqrt3-\sqrt2)/5 You should not use Ferrari to understand the general idea how to bend. But the critical area is very confusing to me – Mikhail G Feb 26 '11 at 21:51
  • $k=5/(3\sqrt3)$ corresponds to the critical value $a/b = \sqrt{29- 6 \sqrt{6}}/5$ where the discriminant is equal zero (I forgot the $1/5$ in the last comment), so we agree there. It seem that you have the solution. What exactly is the question and what is confusing about the critical area? – Fabian Feb 26 '11 at 23:06
  • Dilemma, when a/b is close to 1. kchanges from 1 to C--> the first root of the mentioned polinom ( do not miss the second root t_2>t1 and we need t_1) changes from \sqrt2-1 to 1/\ sqrt, that is t(T(k) is monotonic-> inversion function:k=(1+4t^2-t^2)/(4t). Let s=\tg \beta=a/b & u=b/a->s(k), u(k) --> S(t,a). Find u(t) and finally get S(t,a) - the minumum area of the pentagon to compare with a^2/2 Here you need to do numerical job. If you plot s(t) for (\sqrt2-1,1\sqrt3)&(0.3,0.9), you'll see it. So, there is t_0: t<t_0 we have S<a^2/2->t_0=0459133.., u=1.226958.. 1/u=a/b=0.8150237->\alpha=\pi/4 – Mikhail G Feb 27 '11 at 05:41
  • and \alpha=0.430423... That is confusing Right? Why C is not critical now? – Mikhail G Feb 27 '11 at 05:43
  • Yes, it looks like the pentagon has only minimal area for $0.81 \leq a/b$ afterward the triangle is more optimal. What is confusing now? (yes, $\alpha$ jumps but this can be) – Fabian Feb 27 '11 at 14:52
  • Thank you, but if $a/b <0.81$, the triangle will be the minimum area.Right? 1)Actually the pentagon and triangle have the minimal area for $0.81$, Right? 2)Also $t>t_0$, ie $a/b>0.81$ --> $\alpha=arctg(t_1)$. The jumping was a bit confusing – Mikhail G Feb 27 '11 at 17:17
  • Could you plot the final graph? – Mikhail G Feb 27 '11 at 17:26
  • I do not really know how to plot the graph. As far as I see it $\alpha = \pi/4$ for $a/b < 0.81$ and then it switches over to the solution of the quartic equation (at $a/b=0.81$ there are two solutions with equal area but different shape) -- so got it right. – Fabian Feb 27 '11 at 23:18
  • 1
    Agree, $a/b \approx 0.81$ there are two shapes in the crossing intersaction. Have you ever thought about the sizes of paper towels? Why do they have the particular sizes? I searched for eg German paper towels and found that $a/b>0.81$ (very close to $0.9$ or even $1$. So, do you think the manufacture can slightly reduce a/b with no changes in property of the current paper towels but adding a new one (while bending)? – Mikhail G Feb 28 '11 at 17:59
  • in over words $a/b \approx \sqrt{\frac {2} {3}}$ – Mikhail G Feb 28 '11 at 18:04
  • I have a few ideas of how to minimize your function S but I don't quite understand how you actually found that formula. Could that be explained?

    P.S. I was trying to post an answer and I accidentally posted my comment in the answer section... Vote to delete it, please.

     – Patrick Da Silva May 15 '11 at 01:32
  • There's really something wrong with your formula for the area, for if you fix $b=1$ and fix an arbitrary value for $t$, letting $a$ go to $0$ should make $S$ go to $0$ by geometric considerations, but it goes to $-(t+t^3)$ instead. I'd really like to see how you managed to find that formula. – Patrick Da Silva May 15 '11 at 20:38
  • I do not understand the problem at all. You talk about towels and ratios and areas, but you do not mention the exact facts, and it's confusing. If you want an answer, you should explain the problem better. – Beni Bogosel May 26 '11 at 18:31

1 Answers1

1

The minimum area occurs when $\alpha=\frac{\pi}{4}$ and it is equal to $S_\rm{min}=a^2/2$

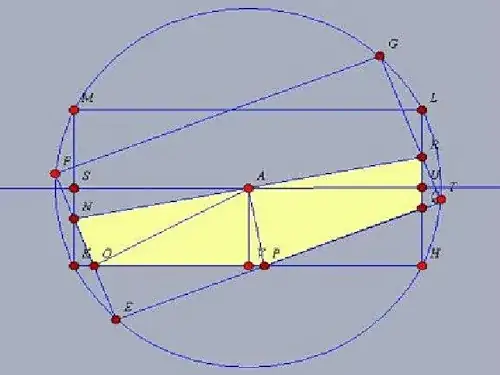
Why? Well I solved this problem using a parametric CAD system and then using geometry. If the height of the towel is $a$ and the width is $b$ with $a<b$ then the critical aspect ratio is $\eta_c=\tan^{-1}\left(\frac{a}{b}\right)$. When the fold angle $\alpha\leq\eta_c$ then the common area is

$$ S_1 = \dfrac{2 a b\cos\alpha-(a^2+b^2)\cos\alpha}{4\cos\alpha (2\cos^2\alpha-1))} $$

but when the fold angle is $\alpha > \eta_c$ then the area is

$$ S_2 = \dfrac{a^2}{4\cos\alpha\sin\alpha} $$

which has a minimum at $\alpha=\pi/4$. The key to the solution is finding the coordinates of the point where the two long sides of the towel intersect after the fold (point $P$ above). This calculates to: $P=(\frac{a}{2}\tan\alpha,\,-\frac{a}{2})$ in a coordinate system in the middle of the towel.

In the end I take the area of half a tower and subtract the triangular parts that stick out. The math I used are based on homogeneous coordinates for the lines, such that a line $L=[A,B,C]$ has an equation equal to $[A,B,C]\cdot[x,y,1]=0$ or $Ax+By+C=0$.

Two points $P$ and $Q$ join with the line $$\rm{JOIN}(P,Q)=\left[P_2-Q_2,Q_1-P_1,P_1 Q_2-P_2 Q_1\right]$$ where $P=(P_1,P_2)=(x_P,y_P)$ and the similarly for $Q$.

Then two lines $L$, $K$ intersect at $$\rm{MEET}(L,K)=\left[\dfrac{L_2 K_3-K_2 L_3}{L_1 K_2 - L_2 K_1}, \dfrac{K_1 L_3 - L_1 K_3}{L_1 K_2 - L_2 K_1}\right]$$ where $L_1$, $L_2$ and $L_3$ are the components of line $L$ and similarly for $K$.

The area of a triangle with vertexes $A$, $B$ and $C$ is

$$ \rm{AREA}(A,B,C) = \frac{1}{2}\left( (B_1-A_1)(C_2-A_2)-(C_1-A_1)(B_2-A_2) \right)$$ that comes from the derivation of the cross product of the vectors $B-A$ and $C-A$.

In addition, the following is true:

  1. The folding line has coordinates $L=[-\sin\alpha,\cos\alpha,0]$.

  2. Point $E$ has coordinates $E=(-\frac{b}{2}\cos2\alpha+\frac{a}{2}\sin2\alpha,\,-\frac{b}{2}\sin2\alpha-\frac{a}{2}\cos2\alpha)$

  3. Point $T$ has coordinates $T=(\frac{b}{2}\cos2\alpha+\frac{a}{2}\sin2\alpha,\,\frac{b}{2}\sin2\alpha-\frac{a}{2}\cos2\alpha)$

John Alexiou
  • 13,816