Does the series $\sum_{n=2}^{\infty}{\frac{\sin(n^3)}{\ln(n)}}$ converge?

Question

Do you have any idea if the series $\sum_{n=2}^{\infty}{\frac{\sin(n^3)}{\ln(n)}}$ converges? I am totally lost!

Answer 1

Heuristically, no, but I don't have a proof. When $n$ is large, $\sin(n^3)$ should behave essentially like independent random numbers in $[-1,1]$ with a certain symmetric distribution. Now if $X_n$ are independent random variables with mean $0$ and variance $\sigma^2 > 0$, $\sum_{n=2}^N X_n/\log(n)$ has variance $\sum_{n=2}^N \sigma^2/\log(n)^2$ which goes to $\infty$ as $N \to \infty$.

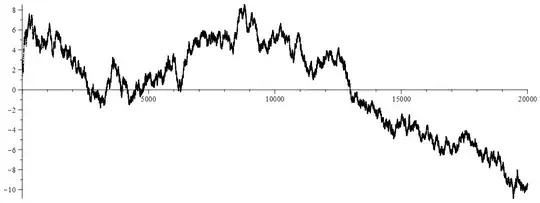
Here's a plot of the partial sums of your series up to $N=20000$. There's no sign of convergence.

{EDIT: new plot using Digits=30]

Answer 2

The series is divergent.

We adopt the result and extend the idea of this posting by Terry Tao: https://mathoverflow.net/questions/201250/is-sum-k-1n-sink2-bounded-by-a-constant-m?sfb=2

The result of the posting is $\sum_{n\leq x} \sin n^3$ is unbounded.

By the unboundedness of $\sum_{n\leq x} \sin n^3$, the abscissa of convergence $\sigma_c$ of $\sum (\sin n^3)/n^s$ satisfies $\sigma_c\geq 0$. If we assume that the series is convergent, then we have the convergence of the Dirichlet series $\sum (\sin n^3)/n^s$ for $\Re(s)>0$. Thus, $\sigma_c=0$ and we have $$ \limsup_{x\rightarrow\infty} \frac{\log |\sum_{n\leq x} \sin n^3|}{\log x} =0. $$ Hence, if the series is convergent, then for any $\epsilon>0$ and $x\geq 1$, there is $C_{\epsilon}>0$ such that $$ |\sum_{n\leq x} \sin n^3|\leq C_{\epsilon} x^{\epsilon}. \ \ (1) $$ We will obtain a contradiction to this statement.

By this posting by David Speyer (based on Weil's inequality): Convergence of $\sum \limits_{n=1}^{\infty}\sin(n^k)/n$ we have an absolute constant $\delta>0$ such that the following hold.

Define $X_1=\sin((k+1)^3)$, $\ldots$, $X_h=\sin((k+h)^3)$ be random variables (as empirical distributions with corresponding outputs for $k=1,\ldots n$ with probability $1/n$ each). We have $$ EX_i=O(n^{-\delta}), \ \text{Var}(X_i)=\frac12 + O(n^{-\delta}), $$ and $$ \text{Var}\sum_{i\leq h} X_i = \frac h2 + O(hn^{-\delta})+2\sum_{1\leq i<j\leq h} \text{Cov}(X_i,X_j)$$ $$ =\frac h2+O(hn^{-\delta})+O(h^2 n^{-\delta}).$$ Let $h=\lceil n^{\delta/2}\rceil$. Assuming all length $h$ partial sums are $O(h^{1/4})$, we have by comparing two estimates of $\text{Var}\sum_i X_i$, $$ \frac h2 + O(h^2 n^{-\delta}) = O(h^{1/2}). $$ These estimates do not agree as $n\rightarrow\infty$. Thus, there is an absolute constant $c>0$ and some length $h$ partial sum of $\sin k^3$ which is $\geq c h^{1/4}$. That is, there is $k\leq n$ such that $$ |\sum_{i\leq h} \sin (k+i)^3| \geq c h^{1/4}\geq c n^{\delta/8}. $$ Since $\sum_{i\leq h} \sin (k+i)^3 = \sum_{j\leq k+h} \sin j^3 - \sum_{j\leq k} \sin j^3$, one of the two partial sums' absolute value on the RHS must satisfy $\geq (c/2) n^{\delta/8}$.

If we take $\epsilon=\delta/9$ in (1), then we have a contradiction.

Therefore, the series is divergent.

Remark

We may explicitly write $\delta$ in terms of the irrationality measure of $\pi$.