Volume by revolution of quadrant of circle about its tangent

Question

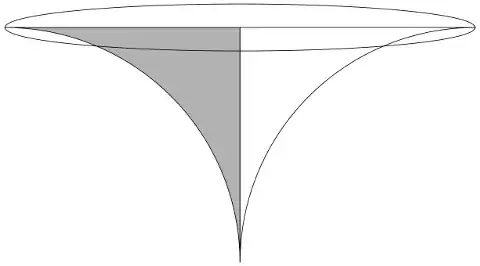
An area bounded by a quadrant of a circle of radius $a$ and the tangents at its extremities revolves about one of the tangents. Find the volume so generated.

I am trying to use this formula: $V=\pi\int_0^a [f(y)]^2dy$

I have used $f(y)=a-\sqrt{a^2-y^2}$

The answer I got is $\pi a^3(\frac{5}{3}-\frac{\pi}{2})$

But shouldn't the required volume be equal to that of a hemisphere that is $\frac{2}{3}\pi a^3$? What am I doing wrong?

To my mind, the required volume occupies the same space as a hemisphere of radius $a$ would. So the answer should've been $\frac{2}{3}\pi a^3$, which is not what I got by integrating. — user464068, Jul 25 '17 at 13:39
Just asking: Have you sketched the region of integration and the volume swept out under rotation? ;) — Andrew D. Hwang, Jul 25 '17 at 13:45
Yes I did. Is there something fundamental that I am missing? If you could just point me? — user464068, Jul 25 '17 at 13:54
I've tried Pappus's Centroid Theorem and obtained $r^{3}\Big(\frac{\pi}{4}-\frac{1}{3}\Big)$ — Kiryl Pesotski, Jul 25 '17 at 14:23

score 1 · Accepted Answer · answered Jul 25 '17 at 14:31

1

"An area bounded by a quadrant of a circle of radius a and the tangents at its extremities" is shaded. The solid swept out by revolving about one of the tangents is not a hemisphere:

answered Jul 25 '17 at 14:31

Andrew D. Hwang

78,195

I feel embarrassed. I had a mental picture stuck to my head. Thank you! – user464068 Jul 25 '17 at 14:52
So to get the required volume all I need to do is subtract the answer I got above,from $\pi a^3$, right? – user464068 Jul 25 '17 at 14:54
I haven't checked the evaluation of your integral, but the set-up (your choice of $f(y) = a - \sqrt{a^{2} - y^{2}}$) is perfectly correct. Separately, we all get mental pictures stuck in mind; even when they're awry, dislodging them is difficult! :) – Andrew D. Hwang Jul 25 '17 at 15:47
1

Thanks a lot! :) – user464068 Jul 26 '17 at 03:25

Volume by revolution of quadrant of circle about its tangent

1 Answers1