Intersections of a Vertical Ellipse and a Rotated Ellipse

Question

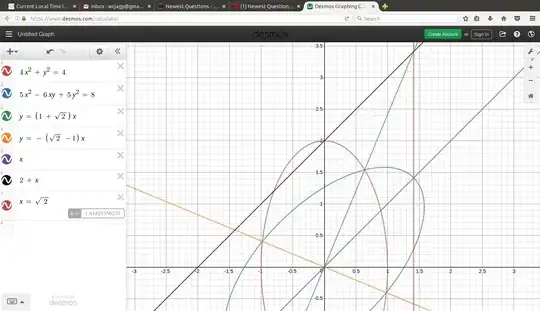
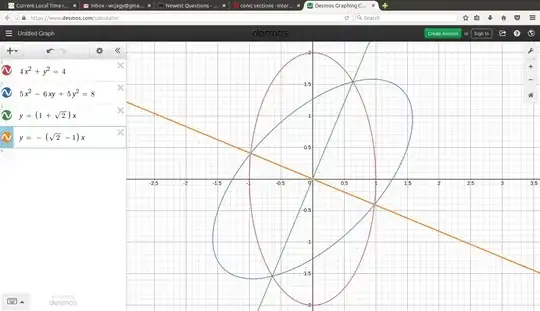
So I'm trying to find the intersections of the equations $$\ {x^2\over 1^2} + {y^2\over 2^2} = 1 $$ $$5x^2 - 6xy + 5y^2 = 8 $$ Both of the equations represent an ellipse, with the first ellipse being a vertical ellipse and the second ellipse being first one rotated 315 degrees counterclockwise. I tried using the elimination method to solve this problem but I don't think I can use it because of the xy term in the second equation. I found this post but I am not sure if this would be useful to help me solve this. My question is what do I need to do in order to find the intersections of these two ellipses? Am I able to continue using the elimination method? Do I have to use a different approach? Or is the post somewhat useful to solve this problem? Edit: Here is a graph of the two equations

Answer 1

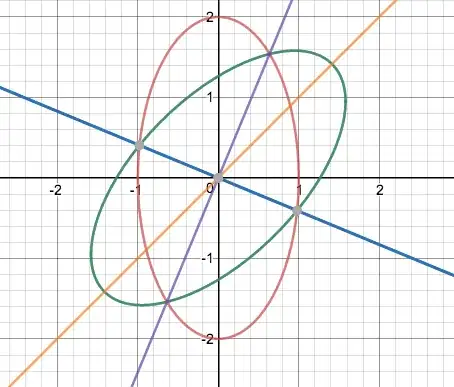
The interesting part is that the ellipses are congruent, and the intersection points are located at rotation half of the given $45^\circ.$ Drawing a certain rhombus tells us that the intersections in the first quadrant occur on the line $y = (\sqrt 2 + 1) x,$ so that $y^2 = (3 + \sqrt 8)x^2.$ Plug that into $4x^2 + y^2 = 4,$ I get $$ x^2 = \frac{4(7 - \sqrt 8)}{41}, \; \; \; y^2 = \frac{4(13 + 4 \sqrt 8)}{41}, $$ $$ x^2 = \frac{28 - 8 \sqrt 2}{41}, \; \; \; y^2 = \frac{52 + 32 \sqrt 2}{41}. $$ Then $4x^2 + y^2 = (112 + 52)/ 41 = 164/41 = 4$

The other pair of intersections are on the line with negative reciprocal slope, $y = -(\sqrt 2 - 1) x,$ so that $y^2 = (3 - \sqrt 8)x^2.$ This time $$ x^2 = \frac{28 + 8 \sqrt 2}{41}, \; \; \; y^2 = \frac{52 - 32 \sqrt 2}{41}. $$

Answer 2

Hint:

Given the symmetry of the problem, you can substitute $y$ from the first to the second equation and you find a biquadratic equation in $x$, that can be solved with the substitution $x^2=t$:

---

from the first equation $$ y^2=4(1-x^2) \quad \rightarrow y=\pm2\sqrt{1-x^2} $$ substituting $$ -5x^2+4=\pm4x\sqrt{1-x^2} $$ squaring $$ 41x^4-56x^2+16=0 $$ so: $$ x^2=\frac{28\pm8\sqrt{2}}{41} $$

and we have the four values $$x=\pm \sqrt{\frac{28\pm8\sqrt{2}}{41}}$$

Answer 3

Rearrange the second equation to $5x^2+5y^2-8= 6xy$, square this equation and substitute $y^2=4(1-x^2)$ ... we get \begin{eqnarray*} 41x^4-56x^2+16=0. \end{eqnarray*} This gives the points of intersection $( \color{blue}{\pm} \sqrt{ \frac{28 \color{red}{+} \sqrt{128}}{41}}, \color{blue}{\pm} \sqrt{2 \frac{13 \color{red}{-} \sqrt{128}}{41}})$ and $( \color{blue}{\pm} \sqrt{ \frac{28 \color{red}{-} \sqrt{128}}{41}}, \color{blue}{\mp} \sqrt{2 \frac{13 \color{red}{+} \sqrt{128}}{41}})$.

Answer 4

HINT: from the second equation we get $$y_{1,2}=\frac{3}{5}x\pm\sqrt{\frac{8}{5}-\frac{16}{25}x^2}$$ this can you insert in the first equation and solve this for $x$ after that you have to solve $$x^2+\frac{1}{4}\left(\frac{3}{5}x+\sqrt{\frac{8}{5}-\frac{16}{25}x^2}\right)^2=1$$

Answer 5

The second ellipse is equivalent to $$(x-y)^2+\frac{(x+y^2)}4=4$$ i.e. $$\dfrac{\bigg(\dfrac {x-y}{\sqrt{2}}\bigg)^2}{1^2}+\dfrac{\bigg(\dfrac {x+y}{\sqrt{2}}\bigg)^2}{2^2}=1$$ with axis of symmetry $y=x$.

As OP pointed out it is the original ellipse rotated clockwise by $\frac \pi4$.

Hence the points of intersection must lie on the lines $$y=x\tan\frac{3\pi}8$$ and $$y=-x\tan\frac {\pi}8$$ .