Improper integral $\int_{0}^{\infty} \frac{x}{e^{x}-1} \ dx$

Question

$$\int_{0}^{\infty} \frac{x}{e^{x}-1}\ dx$$ Is there a way to evaluate this integral without using the zeta function?

Answer 1

METHODOLOGY $1$:

We can write

$$\begin{align} \int_0^\infty \frac{x}{e^x-1}\,dx&=\int_0^\infty \frac{xe^{-x}}{1-e^{-x}}\,dx\\\\ &=\sum_{n=0}^\infty \int_0^\infty xe^{-(n+1)x}\,dx\\\\ &=\sum_{n=1}^\infty \frac1{n^2}\\\\ &=\frac{\pi^2}{6} \end{align}$$

---

METHODOLOGY $2$:

Enforcing the substitution $x=-\log(1-u)$ reveals

$$\begin{align} \int_0^\infty \frac{x}{e^x-1}\,dx&=-\int_0^1 \frac{\log(1-u)}{u}\,du\\\\ &=\text{Li}_2(1)\\\\ &=\frac{\pi^2}{6} \end{align}$$

---

METHODOLOGY $3$:

If one doesn't like either of the first two methodologies, then one can proceed as follows. Begin as in Methodology $2$ and enforce the substitution $x=-\log(1-u)$.

$$\begin{align} \int_0^\infty \frac{x}{e^x-1}\,dx&=-\int_0^1 \frac{\log(1-u)}{u}\,du\\\\ &=\int_0^1\int_0^1 \frac{1}{1-xy}\,dx\,dy\tag 1 \end{align}$$

Then, in THIS ANSWER, I evaluated the double integral in $(1)$ by using the transformation $x=s+t$ and $y=s-t$. This facilitates using real analysis only, and without appealing to special functions to arrive at

$$\int_0^1\int_0^1 \frac{1}{1-xy}\,dx\,dy=\frac{\pi^2}{6}$$

as was to be shown!

Answer 2

By Means of Complex Analysis

We prove the general formula

$$\int^\infty_0 \frac{\sin(ax)}{e^{2\pi x}-1}\,dx = \frac{1}{4}\coth\left(\frac{a}{2} \right)-\frac{1}{2a}$$

Which can be used to generate many values by differentiation with respect to $a$ By integrating the following function

$$f(z) = \frac{e^{iaz}}{e^{2\pi z}-1}$$

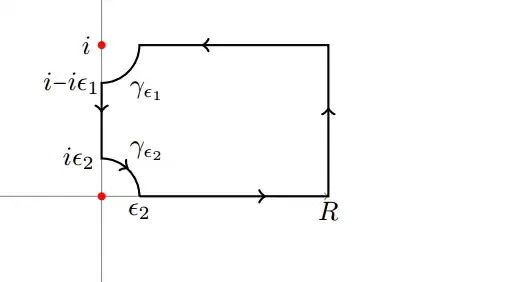
The function is analytic in and on the contour, indented at the poles of the function

Hence by the residue theorem

$$\int_{\gamma_{\epsilon_2}}f(z)\,dz+\int^R_{\epsilon_2}f(x)\,dx+\int^{R+i}_{R}f(x)\,dx\\+\int_{R+i}^{i+\epsilon_2}f(x)\,dx+\int_{\gamma_{\epsilon_1}}f(z)\,dz-\int^{i-i\epsilon_1}_{i\epsilon_2}f(x)\,dx=0$$

Let us first look at with $ R \to \infty $

\begin{align}\left|\int_{R}^{R+i} \frac{e^{iax}}{e^{2\pi x}-1} \,dx\right| &=\left|iR\int^1_0\frac{e^{ia(R+ixR)}}{e^{2\pi (R+ixR)}-1} \,dx\right| \\&\leq R\int^1_0\frac{|e^{ia(R+ixR)}|}{|e^{2\pi (R+ixR)}-1|} \,dx \\&\leq \frac{R}{|e^{2\pi R}-1|} \int^1_0 e^{-axR} \,dx \\&= \frac{1}{a|e^{2\pi R}-1|} (1-e^{-aR}) \sim_{\infty} 0\end{align}

The next integral can be reduced to \begin{align} \int^{i(1-\epsilon_1)}_{i\epsilon_2}\frac{e^{iax}}{e^{2\pi x}-1} \,dx &= i \int^{(1-\epsilon_1)}_{\epsilon_2}\frac{e^{-ax}}{e^{2\pi i x}-1} \,dx \\&= \frac{1}{2}\int^{(1-\epsilon_1)}_{\epsilon_2}\frac{e^{-ax}}{\sin(\pi x) e^{i\pi x}} \,dx \\ &= \frac{1}{2}\int^{(1-\epsilon_1)}_{\epsilon_2}\frac{e^{-ax}}{\sin(\pi x) e^{i\pi x}} \,dx \\ &= \frac{1}{2}\int^{(1-\epsilon_1)}_{\epsilon_2}\frac{\cos(\pi x)}{\sin(\pi x) }e^{-ax} \,dx-\frac{i}{2}\int^{(1-\epsilon_1)}_{\epsilon_2}e^{-ax} \,dx\end{align}

Since the first integral diverges when $ \epsilon_1,\epsilon_2 \to 0 $

$$ PV\int^{i}_{0}\frac{e^{iax}}{e^{2\pi x}-1} \,dx =PV \int^{1}_{0}\frac{\cos(\pi x)}{2\sin(\pi x) }e^{-ax} \,dx-i\frac{1-e^{-a}}{2a} $$

The remaining integrals can be evaluated using residues $$\lim_{\epsilon_2 \to 0} \int_{\gamma_{\epsilon_2}}f(z)\,dz = -\frac{\pi i}{2}\mathrm{Res}(f,0)= -\frac{i}{4}$$

$$\lim_{\epsilon_1 \to 0} \int_{\gamma_{\epsilon_1}}f(z)\,dz = -\frac{\pi\,i}{2}\mathrm{Res}(f,i)= -\frac{i}{4}e^{-a}$$

By combining the results together

$$PV\int^\infty_{0}\frac{e^{iax}}{e^{2\pi x}-1}\,dx -PV\int^\infty_{0}\frac{e^{ia(x+i)}}{e^{2\pi (x+i)}-1}\,dx \\-PV \int^{1}_{0}\frac{\cos(\pi x)}{2\sin(\pi x) }e^{-ax} \,dx+i\frac{1-e^{-a}}{2a} = i\frac{e^{-a}+1}{4}$$

Which reduces to

$$(1-e^{-a})PV\int^\infty_{0}\frac{e^{iax}}{e^{2\pi x}-1}\,dx -PV \int^{1}_{0}\frac{\cos(\pi x)}{2\sin(\pi x) }e^{-ax} \,dx = i\frac{e^{-a}+1}{4}-i\frac{1-e^{-a}}{2a}$$

By equating the real part

$$\int^\infty_0 \frac{\sin(ax)}{e^{2\pi x}-1}\,dx = \frac{1}{4}\coth\left(\frac{a}{2} \right)-\frac{1}{2a}$$

Now by differentiation and letting $a \to 0 $

$$\int^\infty_0 \frac{x}{e^{2\pi x}-1}\,dx = \frac{1}{24}$$

Then the result follows by $y = 2\pi x$.

Answer 3

$$\text{ if } L(f) = F(s) \implies \int_0^{\infty} \frac f{e^t-1}dt = \sum_{s\ge1} F(s)$$ $$L(t) =\frac 1{s^2}\implies\int_0^{\infty} \frac t{e^t-1}dt = \sum_{s\ge1}\frac 1{s^2} = \zeta(2) $$