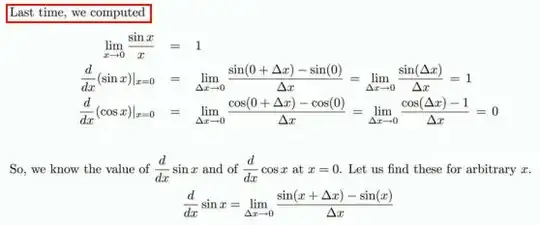1

I'm watching Lecture 3 in MIT single variable calculus. https://www.youtube.com/watch?v=kCPVBl953eY&list=PL590CCC2BC5AF3BC1&index=3

And at one point the instructor does the following:

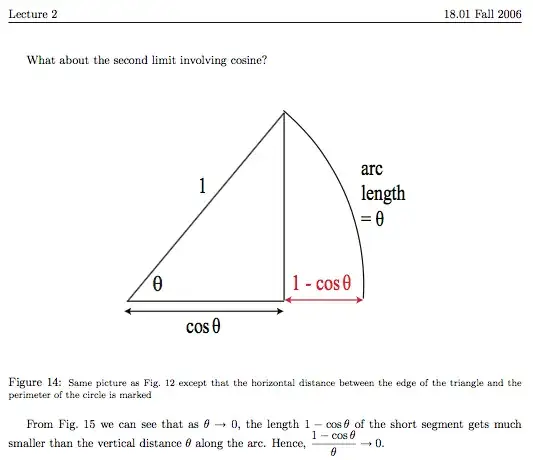
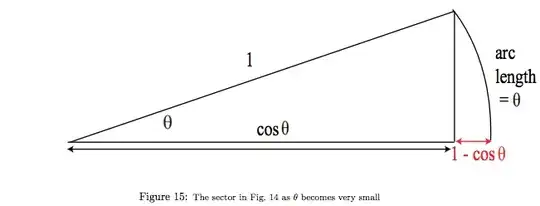
enter image description here

I was under the impression that when evaluating limits we need to avoid having $0/0$ in the denominator. However, in the notes here, it says that

$\frac{\cos\Delta x - 1 }{\Delta x} \to 0$

How does this work?

bugsyb
  • 177
  • 7

7 Answers7

3

[This answer is more about how to read when using online sources for self-directed study than directly answering your question.]

You have had the solution on hand. The excerpt you put in the question is from the lecture note of Lecture 3. The professor explicitly mentions in the first page of the note that

enter image description here

You should refer back to the "last lecture" (Lecture 2)— it is done on page 10:

enter image description here enter image description here

[Added later:]Remark. Note that this lecture note only gives a "plausible" argument why the results are true. You would learn in real analysis what a rigorous proof should look like and that would be another story.

  • Yes. I have just added a remark about that. I'm assuming one would see lots of such "non-rigorous" proof later when using this serie of MIT lecture notes, which could be a motivation to learn real analysis. –  Jul 17 '17 at 15:57
  • Ok no issues. Will delete the comment as it is no longer necessary. – Paramanand Singh Jul 17 '17 at 15:58
1

HINT: write your Quotient in the form $$\frac{(\cos(\Delta x)-1)(\cos(\Delta x)+1)}{\Delta x(\cos(\Delta x)+1)}$$

Dr. Sonnhard Graubner
  • 95,283
1

hint

$$1-\cos (d)=2\sin^2(\frac {d}{2}) $$

$$|\cos (d)-1|\le \frac {d^2}{2} $$ if we know that

$$|\sin (A)|\le | A |$$ hence $$\Bigl |\frac {\cos (\Delta x)-1}{\Delta x}\Bigr |\le \frac {|\Delta x|}{2} $$

hamam_Abdallah
  • 62,951
0

By the mean value theorem, $$\frac{\cos\Delta x-1}{\Delta x}=\frac{\cos\Delta x-\cos(0)}{\Delta x-0}=-\sin(c)$$ for some $c\in (0,\Delta x)$

Let $\Delta x \rightarrow0$ and see what happens.

An alternative way of computing the limit:

$$\frac{\cos\Delta x-1}{\Delta x}=\frac{\cos^2\Delta x-1}{\Delta x\cdot(\cos\Delta x+1)}=\frac{\sin^2\Delta x}{\Delta x\cdot(\cos\Delta x+1)}=\frac{\sin\Delta x}{\Delta x}\cdot \frac{\sin \Delta x}{\cos\Delta x+1}$$

Now, as $\Delta x\rightarrow0$, by continuity and the known fact that

$$\lim_{\Delta x\rightarrow 0}\frac{\sin\Delta x}{\Delta x}=1$$

we get

$$\lim_{\Delta x\rightarrow 0}\frac{\sin\Delta x}{\Delta x}\cdot \frac{\sin \Delta x}{\cos\Delta x+1}=1\cdot\frac{0}{2}=0.$$

dromastyx
  • 2,796
  • 1
    ?! This limit is by definition $\cos'(0)$. You are using the mean value theorem (which involves computing the derivative $\cos'$) to argue about this limit? This is as circular as it gets. – Clement C. Jul 17 '17 at 15:47
  • @ClementC. I thought that the original problem the OP had was that the limit was of the form "0/0". I assumed that he knew that $\cos'(x)=-\sin(x)$, which is not hard to prove. – dromastyx Jul 17 '17 at 15:58
  • Look at the limit: it is exactly the definition of $\cos' 0$. – Clement C. Jul 17 '17 at 16:00
  • @ClementC. Yes, it is. – dromastyx Jul 17 '17 at 16:00
  • @ClementC. Note that I only assumed that $\cos'(c)=-\sin(c)$ for some $c\in(0,\Delta x)$. – dromastyx Jul 17 '17 at 18:50
0

Since you know that

$$\lim_{x \rightarrow 0}\frac{\cos x -1}{x}=\lim_{x \rightarrow 0}\frac{\cos^2\frac{x}{2}-\sin^2\frac{x}{2}-1}{x} $$

$$\lim_{x \rightarrow 0}\frac{\cos^2\frac{x}{2}-\sin^2\frac{x}{2}-1}{x} =\lim_{x \rightarrow 0}\frac{-\sin^2\frac{x}{2}-\sin^2\frac{x}{2}}{x}$$

$$\lim_{x \rightarrow 0}\frac{-\sin^2\frac{x}{2}-\sin^2\frac{x}{2}}{x}=\lim_{x \rightarrow 0}\frac{-2\sin^2\frac{x}{2}}{x}$$

$$ \lim_{x \rightarrow 0}\frac{-2\sin^2\frac{x}{2}}{x}=\lim_{x \rightarrow 0}-\sin\frac{x}{2}\frac{\sin \frac{x}{2}}{\frac{x}{2}}$$

$$\lim_{x \rightarrow 0}-\sin\frac{x}{2}\frac{\sin \frac{x}{2}}{\frac{x}{2}}=\lim_{x \rightarrow 0}-\sin\frac{x}{2}$$

$$\lim_{x \rightarrow 0}-\sin\frac{x}{2}=0$$

Crazy
  • 2,125
0

Suppose you know the limit exists. Then by symmetry,

$$L=\lim_{x\to0}\frac{\cos(x)-1}x=\lim_{x\to0}\frac{\cos(-x)-1}{-x}$$

The second limit simplifies into

$$-\lim_{x\to0}\frac{\cos(x)-1}x$$

Finally, add these together to get

$$L+L=0\implies L=0$$

Simply Beautiful Art
  • 74,685
0

Using the fact that $\lim\limits_{\Delta x\to0}\frac{\sin(\Delta x)}{\Delta x}=1$ (as shown in this answer) $$ \begin{align} \lim_{\Delta x\to0}\frac{\cos(\Delta x)-1}{\Delta x} &=\lim_{\Delta x\to0}\frac{\cos(\Delta x)-1}{\sin(\Delta x)}\frac{\sin(\Delta x)}{\Delta x}\\ &=\lim_{\Delta x\to0}\frac{\cos(\Delta x)-1}{\sin(\Delta x)}\lim_{\Delta x\to0}\frac{\sin(\Delta x)}{\Delta x}\\ &=-\lim_{\Delta x\to0}\frac{\sin(\Delta x)}{\cos(\Delta x)+1}\lim_{\Delta x\to0}\frac{\sin(\Delta x)}{\Delta x}\\ &=-\frac02\cdot1 \end{align} $$

robjohn
  • 345,667