Why is $\sqrt{8}/2$ equal to $\sqrt{2}$?

Question

I am trying to help my daughter on her math homework and I am having some trouble on some equation solving steps. My current major concern relies on understanding why $\sqrt{8}/2$ equal to $\sqrt{2}$.

Thanks in advance

Answer 1

I am a bit surprised that nobody suggested $$\left({\frac{\sqrt 8}2}\right)^2 = \frac{{\left(\sqrt 8\right)}^2}{2^2} = \frac84 = 2. $$

Answer 2

It isn't, as originally written. To see why the fixed version is correct, we have:

$$\frac{\sqrt{8}}2=\frac{\sqrt{4\cdot2}}2=\frac{\sqrt{4}\sqrt{2}}2=\frac{2\sqrt{2}}2=\sqrt{2}.$$

Answer 3

It’s simple:

$$\frac{\sqrt{8}}{2} = \frac{\sqrt{2 \cdot 2 \cdot 2}}{\sqrt{2 \cdot 2}} = \sqrt{2}$$

:)

Answer 4

$$\frac{\sqrt8}{2}=\frac{\sqrt8}{\sqrt{2^2}}=\sqrt{\frac{8}{2^2}}=\sqrt{\frac{8}{4}}=\sqrt2.$$

Answer 5

By noting that $2^3 =8$, you have $$\frac{\sqrt{8}}{2} = \frac{\sqrt{2^3}}{2} = \frac{ 2^{3/2}}{2} = 2^{1/2}=\sqrt{2} \neq \sqrt{4}$$

Answer 6

Geometric approach:

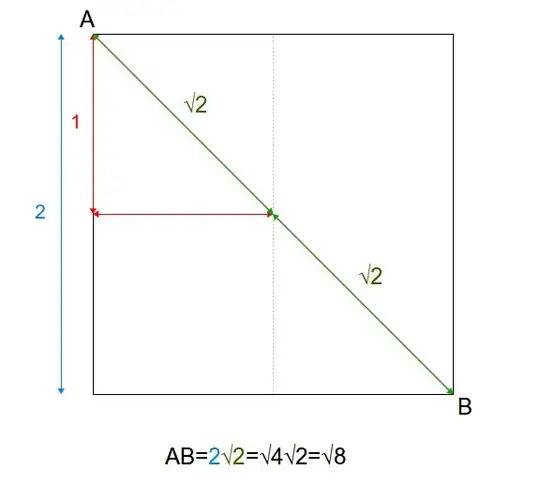
Now what is $\displaystyle\text{AB}/2$ ?

Answer 7

Other techniques to prove that result:

---

Technique $\mathbf 1$:

We may also prove that by solving this equation for $x$:

$$\begin{align}\frac{\sqrt x}{2}&=\sqrt2\\\sqrt x&=2\sqrt 2\\\left(\sqrt x\right)^2&=\left(2\sqrt 2\right)^2\\x&=4\cdot2=\color{green}{\boxed{\color{black}{8}}}\end{align}$$

Therefore: $$\frac{\sqrt8}{2}=\sqrt 2$$ I know, this is a terrible way. But hey, it works! ;-)

---

Technique $\mathbf 2$:

Just like in Technique $\mathbf 1$: We may also prove that result by solving this equation for $x$:

$$\begin{align}\frac{\sqrt 8}{2}&=\sqrt x\\ \left(\frac{\sqrt 8}{2}\right)^2&=\sqrt x^2\\ \frac84&=x \implies x=\color{green}{\boxed{\color{black}2}} \end{align}$$

Therefore: $$\frac{\sqrt8}{2}=\sqrt 2$$

---

Technique $\mathbf 3$:

If $a=b$ then this means $a-b=0$, and the opposite is true. So let's check for $\sqrt 2$ and $\sqrt 8/2$:$$\begin{align}\dfrac{\sqrt 8}{2}-\sqrt{2}&=\dfrac{\sqrt 8}{2}-\left(\sqrt{2} \cdot \dfrac{\sqrt{4}}{2}\right)\quad\to\quad\text{since $\sqrt 4=2$}\\ &=\dfrac{\sqrt 8}{2}-\dfrac{\sqrt 2\cdot\sqrt 4}{2}\\ &=\dfrac{\sqrt{8}-\sqrt{2}\cdot\sqrt{4}}{2}\\ &=\dfrac{\sqrt{8}-\sqrt{2\cdot4}}{2}\\ &=\dfrac{\sqrt 8-\sqrt 8}{2}=\dfrac{0}{2}=0 \end{align}$$ Therefore, we can easily conclude that: $$\dfrac{\sqrt 8}{2}=\sqrt 2$$

---

Technique $\mathbf 4$:

If $a=b$ then it follows that $a/b=1$, and the opposite is true. So let's check for $\sqrt 2$ and $\sqrt 8/2$: $$\begin{align}\dfrac{\sqrt2}{\dfrac{\sqrt8}{2}}&=\sqrt{2}\cdot\dfrac{2}{\sqrt{8}}=\dfrac{\sqrt2\cdot\sqrt 4}{\sqrt8}=\dfrac{\sqrt{2\cdot 4}}{\sqrt 8}=\dfrac{\sqrt8}{\sqrt8}=1 \end{align}$$ Therefore: $$\dfrac{\sqrt 8}{2}=\sqrt 2$$

---

Technique $\mathbf 5$:

We will do a proof by contradiction: We suppose that $\sqrt 8/2\ne\sqrt 2$, therefore there must be a difference between them which is not zero $\sqrt 8/2-\sqrt 2\ne0$, that we will call $x$. So let's check if $x\ne0$: $$\begin{align}x=\dfrac{\sqrt 8}{2}-\sqrt{2}&=\dfrac{\sqrt 8}{2}-\left(\sqrt{2} \cdot \dfrac{\sqrt{4}}{2}\right)\\ &=\dfrac{\sqrt 8}{2}-\dfrac{\sqrt 2\cdot\sqrt 4}{2}\\ &=\dfrac{\sqrt{8}-\sqrt{2}\cdot\sqrt{4}}{2}\\ &=\dfrac{\sqrt{8}-\sqrt{2\cdot4}}{2}\\ &=\dfrac{\sqrt 8-\sqrt 8}{2}=\dfrac{0}{2}=0 \end{align}$$But this is a contradiction, since $x$ must be non-zero but it turns out that it is equal to $0$. Therefore: $$\dfrac{\sqrt 8}{2}=\sqrt 2$$

---

Generalization: Let $x$ be a strictly positive number in $\Bbb R$, then: $$\dfrac{\sqrt{x^3}}{x}=\sqrt{x}$$

Proof: $$\dfrac{\sqrt{x^3}}{x}=\dfrac{\sqrt{x^3}}{\sqrt{x^2}}=\sqrt{\dfrac{x^3}{x^2}}=\sqrt x\qquad\blacksquare\\\,\\\textit{inspired by Paul Dirac's post :)}$$

Answer 8

$\sqrt{8} = \sqrt{4\cdot2} = \sqrt{4}\cdot\sqrt{2} = 2 \sqrt{2}$ in the numerator. Cancel the $ 2 $ in both the numerator and the denominator to obtain the required result.