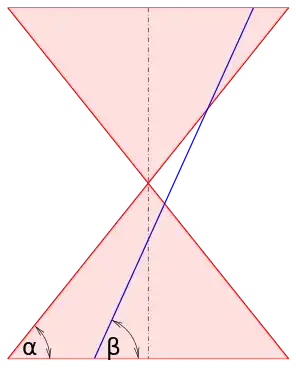
The definition of the eccentricity of a conic section given in Wikipedia is $\dfrac {\sin \beta}{\sin\alpha}$ where $\alpha$ and $\beta$ are angles of incline from the horizontal of the slant of the cone and the cutting plane respectively.
(see diagram below from Wikipedia)
For an ellipse with semi-major and semi-minor axes $a,b$ the eccentricity is $e=\dfrac{\sqrt{a^2-b^2}}a$. This can easily be proven using the focus-directrix definition.
How can it be shown that the first definition is equivalent to the second, i.e. $$e=\frac{\sin \beta}{\sin\alpha}=\dfrac{\sqrt{a^2-b^2}}a$$
The challenge here is that the first and and second definitions are based on dimensions in different planes.
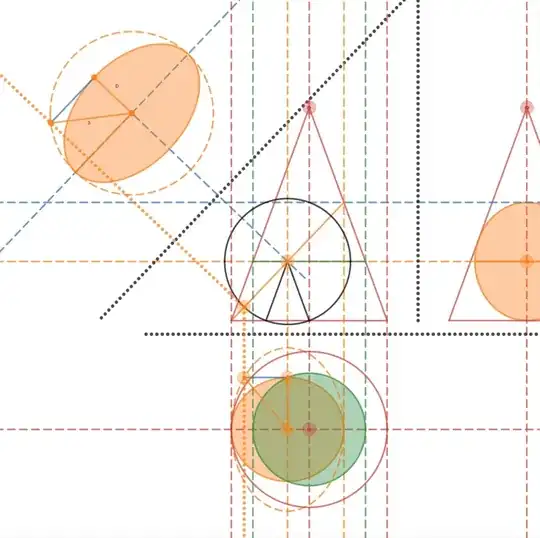
Addendum (27 Jul 2017)
Here's a desmos implementation of simulated orthographic projections of the conic section described above. The short blue line on the plane of the ellipse has length $\sqrt{a^2-b^2}$. From the diagram it can be seen that this is equal in length to the short black line, which has length $\dfrac {a\sin\alpha}{\sin\beta}$. Equating and diving by $a$ gives the required result.