1

I am trying to obtain $$\lim_{x\to0}\frac{\Phi^{-1}(1-x)}{\Phi^{-1}(1-x/n)}$$ where $\Phi^{-1}$ is the inverse cdf of the standard normal distribution and $n>0$. As there is an indeterminate form ($\infty/\infty$), I am applying l'Hôpital's rule, but the resulting expression (I mean, of the derivatives of both the numerator and denominator) is of the form $\infty/\infty$ as well. Would you give me any advice on how to proceed?

Dhruv Kohli
  • 5,216
Cromack
  • 299

2 Answers2

2

This answer is not complete and needs correction. I am stuck at a point and will update this answer soon. However, I am retaining this answer in hope that someone might state more clearly the transition from equation (a) to equation (b).

$$1-x = \Phi(t) = \frac{1}{2} + \frac{1}{2}\text{erf}\left(\frac{t}{\sqrt{2}}\right) \implies \Phi^{-1}(1-x) = \sqrt{2}\ \text{erf}^{-1}(1-2x)$$

Similarly,

$$\Phi^{-1}\left(1-\frac{x}{n}\right) = \sqrt{2}\ \text{erf}^{-1}\left(1-\frac{2x}{n}\right)$$

where,

$$\text{erf}^{-1}(u) = \sum_{k=0}^{\infty}\frac{c_k(\sqrt{\pi}/2)^{2k+1}}{2k+1}u^{2k+1}$$

Note that $\text{erf}^{-1}(0) = 0$.

$$\begin{align}\lim_{x\rightarrow 0} \frac{\Phi^{-1}(1-x)}{\Phi^{-1}\left(1-\frac{x}{n}\right)} &= \lim_{x\rightarrow 0} \frac{\sqrt{2}\ \text{erf}^{-1}(1-2x)}{\sqrt{2}\ \text{erf}^{-1}\left(1-\frac{2x}{n}\right)} = \lim_{x\rightarrow 0} \frac{ \text{erf}^{-1}(1-2x)}{\ \text{erf}^{-1}\left(1-\frac{2x}{n}\right)}-1+1 \\\\ &= \lim_{x\rightarrow 0} \frac{ \text{erf}^{-1}(1-2x) - \text{erf}^{-1}\left(1-\frac{2x}{n}\right)}{\text{erf}^{-1}\left(1-\frac{2x}{n}\right)}+1 \\\\ &= \lim_{x\rightarrow 0} \frac{\sum_{k=0}^{\infty}\frac{c_k(\sqrt{\pi}/2)^{2k+1}}{2k+1}\left((1-2x)^{2k+1} - \left(1-\frac{2x}{n}\right)^{2k+1}\right)}{\text{erf}^{-1}\left(1-\frac{2x}{n}\right)} + 1\\\\ &= \lim_{x\rightarrow 0} \frac{\sum_{k=0}^{\infty}\frac{c_k(\sqrt{\pi}/2)^{2k+1}}{2k+1}\left(2x(\frac{1}{n}-1)(\sum_{i=0}^{2k}(1-2x)^{i}(1-\frac{2x}{n})^{2k-i})\right)}{\text{erf}^{-1}\left(1-\frac{2x}{n}\right)} + 1 \\\\ &= \frac{\sum_{k=0}^{\infty}\frac{c_k(\sqrt{\pi}/2)^{2k+1}}{2k+1}\left((\rightarrow 0)(\rightarrow (2k+1)\right)}{\rightarrow \infty} + 1 \tag{a} \\\\ &= \rightarrow 0 + 1 = 1 \tag{b} \end{align}$$

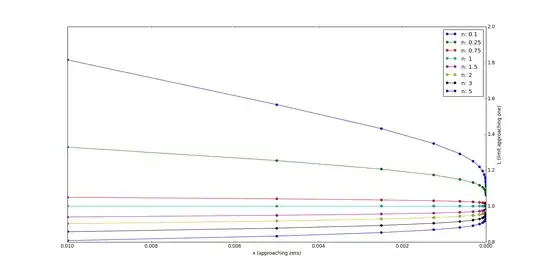
Note: How did I get ($\rightarrow 0$)? It turns out that the numerator can be upper bounded by $2x(1/n-1)$ times derivative of $\text{ erf}^{-1}(u)$ evaluated at $u=(1-2x/\max(1,n))$, where $x \rightarrow 0$. Now, although the numerator has form of $(\rightarrow 0)(\rightarrow \infty)$ and the denominator is tending to $\infty$ as $x \rightarrow 0$. Near $0^+$, the rate(speed) with which the denominator is tending to $\infty$ is much faster than the rate at which numerator is tending to $\infty$ due to the multiplication of $(\rightarrow 0)$ in the numerator. I observed this by plotting the function for different values of $n$ and the function is approaching $0$ as $x \rightarrow 0$. However, concretely proving this seems to me to be non trivial.

Some equations that might be useful to solve.

$$\frac{\partial \text{ erf}^{-1}(u)}{\partial u} = \sum_{k=0}^{\infty}c_k(\sqrt{\pi}/2)^{2k+1}u^{2k} = \frac{\sqrt{\pi}}{2}e^{(\text{erf}^{-1}(u))^2}$$

$$\lim_{u\rightarrow 0}u\frac{\partial \text{ erf}^{-1}(u)}{\partial u} = \lim_{u\rightarrow 0} \sum_{k=0}^{\infty}c_k(\sqrt{\pi}/2)^{2k+1}u^{2k+1} = \lim_{u\rightarrow 0}u\frac{\sqrt{\pi}}{2}e^{(\text{erf}^{-1}(u))^2} = (\rightarrow 0)(\rightarrow \sqrt{\pi}/2)$$

Check this wiki page for more information on $\text{erf}^{-1}$ and its taylor series.

Check this wolfram page for a closed formula for the derivative of $\text{erf}^{-1}(u)$. It is easy to derive it from the definition of $\text{erf}^{-1}(u)$ in the integral form.

With simulations using different values of $n$, I get convergence to $1$.

enter image description here

Dhruv Kohli
  • 5,216
  • I can't fully see how you get the last limit from the previous one. Shouldn't it be $2x(\frac{1}{n}-1)$ instead of $2x(1-\frac{1}{n})$ in the last limit? – Cromack Jul 11 '17 at 07:46
  • @Cromack Yes you are right. That should be $2x(\frac{1}{n}-1)$ and then as $x\rightarrow 0$ the numerator will tend to $0$ and denominator will tend to $\infty$. Any other doubt? By the way I found the question very interesting. – Dhruv Kohli Jul 11 '17 at 08:01
  • Yes, I have another question: is the identity $(1-2x)^{2k+1}-(1-\frac{2x}{n})^{2k+1} = 2x(\frac{1}{n}-1)(\sum_{i=0}^{2k}(1-2x)^i(1-\frac{2x}{n})^{2k-i})$ a well-known identity? And might the second exponent of the sum just be $i$ instead of $2k-i$? Sorry, that was two questions :) – Cromack Jul 11 '17 at 08:35
  • Wait I did a mistake in my comment. $a^{2k+1}-b^{2k+1} = (a-b)(\sum_{i=0}^{2k}a^ib^{2k-i})$ – Dhruv Kohli Jul 11 '17 at 08:40
  • Hi again, @expiTTp1z0. I have another question: does the sum of the $c_k$ terms in the Taylor series converge? I mean, does it equal a finite number? – Cromack Jul 11 '17 at 15:21
  • @Cromack Check the Taylor series expansion of $\text{erf}^{-1}(z)$ on the wiki page. Now, as $z \rightarrow 1$, $\text{erf}^{-1}(z) \rightarrow \infty$ but in above equation $z \rightarrow 0$ (due to $2x(1-1/n) \rightarrow 0$) in which case $\text{erf}^{-1}(z) \rightarrow 0$. – Dhruv Kohli Jul 11 '17 at 15:33
  • And wouldn't that be an indeterminate form $0\cdot\infty$? – Cromack Jul 11 '17 at 18:27
  • Here is what I am thinking. So, if you see the tailor series expansion of $\text{erf}^{-1}(z)$ on the wiki link and remove the $2k+1$ terms from the denominator in the summation and then approach $z$ to $0$, will the resulting limit of function be $0$. If yes then the numerator will approach to $0$. – Dhruv Kohli Jul 11 '17 at 19:11
  • I can see that, but the $c_k$ terms $\to\infty$, right? According to Wikipedia, $c_k={1,1,\frac{7}{6},\frac{127}{90},\ldots}$. – Cromack Jul 11 '17 at 19:37
  • Why is it that, "in the limit, the numerator will become $u$ times the derivative of $\mathrm{erf}^{-1}(u)$"? – Cromack Jul 11 '17 at 20:31
  • $\lim_{u\rightarrow 0} \sum_{k=0}^{\infty}c_k(\sqrt{\pi}/2)^{2k+1}u^{2k+1} = \sum_{k=0}^{\infty}c_k(\sqrt{\pi}/2)^{2k+1}(\rightarrow 0)$. Now compare this with the numerator that we were trying to find the limit of. Did you get it? – Dhruv Kohli Jul 11 '17 at 20:34
  • Yes, but what about the denominator $2k+1$ in the original limit we're trying to find? – Cromack Jul 11 '17 at 20:44
  • That cancels out with the $\rightarrow(2k+1)$ term in the numerator, ofcourse, in the limit. Got it? – Dhruv Kohli Jul 11 '17 at 20:46
  • I can see it now! Amazing, truly! Thanks for all the effort :) – Cromack Jul 11 '17 at 20:48
  • Happy to help. It was a nice question. I wonder if there is a simpler proof. I think Taylor expansion will be inevitable at some point in the proof. – Dhruv Kohli Jul 11 '17 at 20:49
  • @Cromack 200 rep cap achieved. Try upvoting after 3 hours. Thanks! – Dhruv Kohli Jul 11 '17 at 21:02
  • I've revisited this and I'm afraid I can't see it today... In the last limit, you have $2x(1/n-1)\times S$, where $S\to2k+1$ as $x\to0$. Such a fact cancels the $2k+1$ denominator, so you still have $2x(1/n-1)\to0$ as $x\to0$. Now, I assume that $u=2x(1/n-1)$ and then I can't follow your line of thought in the argument of the derivative... – Cromack Jul 12 '17 at 08:44
  • @Cromack I am also revisiting the proof to find possible mistakes. – Dhruv Kohli Jul 12 '17 at 09:13
  • Then, the derivative is $u^{2k-1}$ times the numerator, isn't it? – Cromack Jul 12 '17 at 09:26
  • Yes. That's right. But I think there is an important point missing. I am working on it. – Dhruv Kohli Jul 12 '17 at 09:39
  • I think I made another mistake. It boils down to showing that as $x \rightarrow 0$, $x(e^{(\text{erf}^{-1}(1-2x))^2})/(\text{erf}^{-1}(1-2x)) \rightarrow 0$. Check this wolfram plot. By plot it does approach $0$ but to show it in mathematical equations will require some more thinking. – Dhruv Kohli Jul 12 '17 at 10:39
  • I think I have it:

    $\lim_{x\to0}\sum_{k=0}^\infty c_k\left(\frac{\sqrt{\pi}}{2}\right)^{2k+1}xR\frac{S}{2k+1}$, where $R=2(1/n-1)$ and $S$ is the sum from $0$ to $2k$. That limit is equal to $\lim_{x\to0}\sum_{k=0}^\infty\frac{\partial\mathrm{erf}^{-1}(x)}{\partial x}\frac{1}{x^{2k-1}}R\frac{S}{2k+1}=(\to\frac{\sqrt{\pi}}{2})(\to1/\infty=0)(\to R)(\to 1)=0$. Is that correct?

     – Cromack Jul 12 '17 at 11:01
  • The derivative itself is a summation with terms having odd powers of $x$. So your argument doesn't seem right to me. I think I do understand how the whole term (num/denom) will approach zero. It is difficult to explain in a comment. I am trying to write in mathematical terms. But getting stuck at a point. Please wait for sometime. Thanks for your patience. – Dhruv Kohli Jul 12 '17 at 11:13
  • You're right! What about $\lim_{x\to0}\frac{\partial\mathrm{erf}^{-1}(x)}{\partial x}\sum_{k=0}^\infty \frac{1}{x^{2k-1}}R\frac{S}{2k+1}$? – Cromack Jul 12 '17 at 11:19
  • This limit does not seem to be relevant to me. Check another answer that I added. I'll update this answer after correcting it. Thanks. – Dhruv Kohli Jul 12 '17 at 13:32
  • Why is it not relevant to you? Is it not true that $\lim_{x\to0}\sum_{k=0}^\infty c_k\left(\frac{\sqrt{\pi}}{2}\right)^{2k+1}xR\frac{S}{2k+1}=\lim_{x\to0}\frac{\partial\mathrm{erf}^{-1}(x)}{\partial x}\sum_{k=0}^\infty\frac{1}{x^{2k-1}}R\frac{S}{2k+1}$? If not, I understand it's not relevant. – Cromack Jul 12 '17 at 16:25
  • I haven't computed the actual values of the limit but the functions on the two sides are not the same. – Dhruv Kohli Jul 12 '17 at 16:52
1

Here is another much simpler way to solve.

Note that,

$$\frac{\partial \Phi^{-1}(x)}{\partial x} = \frac{1}{\phi(\Phi^{-1}(x))} \ \ \text{ and } \ \ \frac{\partial \Phi^{-1}(x/n)}{\partial x} = \frac{1}{n\phi(\Phi^{-1}(x/n))}$$

Also,

$$\frac{\partial \phi(\Phi^{-1}(x))}{\partial x} = \frac{-\Phi^{-1}(x)\phi(\Phi^{-1}(x))}{\phi(\Phi^{-1}(x))} = -\Phi^{-1}(x) $$

$$ \frac{\partial \phi(\Phi^{-1}(x/n))}{\partial x} = \frac{-\Phi^{-1}(x/n)\phi(\Phi^{-1}(x/n))}{n\phi(\Phi^{-1}(x/n))} = -\frac{\Phi^{-1}(x/n)}{n}$$

$$\begin{align} L &= \lim_{x \rightarrow 0} \frac{\Phi^{-1}(1-x)}{\Phi^{-1}(1-x/n)} = \lim_{x \rightarrow 0} \frac{-\Phi^{-1}(x)}{-\Phi^{-1}(x/n)} = \color{red}{\lim_{x \rightarrow 0} \frac{\Phi^{-1}(x)}{\Phi^{-1}(x/n)}} = \frac{\rightarrow -\infty}{\rightarrow -\infty}\\\\ &= \lim_{x \rightarrow 0} \frac{\frac{\partial \Phi^{-1}(x)}{\partial x}}{\frac{\partial \Phi^{-1}(x/n)}{\partial x}} = \lim_{x \rightarrow 0} \frac{n\phi(\Phi^{-1}(x/n))}{\phi(\Phi^{-1}(x))} = \frac{\rightarrow 0}{\rightarrow 0} \\\\ &= \lim_{x \rightarrow 0} \frac{n\frac{\partial \phi(\Phi^{-1}(x/n))}{\partial x}}{\frac{\partial \phi(\Phi^{-1}(x))}{\partial x}} = \color{red}{\lim_{x \rightarrow 0} \frac{\Phi^{-1}(x/n)}{\Phi^{-1}(x)}} = 1/L \end{align}$$

Therefore,

$$L^2 = 1 \implies L = \pm 1$$

Clearly, $L$ cannot be negative, so $L=1$.

Dhruv Kohli
  • 5,216
  • Is $\phi$ the pdf of the standard normal distribution? – Cromack Jul 12 '17 at 16:26
  • Yes. It is the pdf of standard normal distribution. – Dhruv Kohli Jul 12 '17 at 16:47
  • I have one question: $\frac{\partial \Phi^{-1}(x)}{\partial x}=\frac{\partial \Phi^{-1}(1-x)}{\partial x}$? – Cromack Jul 12 '17 at 17:29
  • Where did I use it? Note that $\Phi(-y) = 1 - \Phi(y)$. Take $y = \Phi^{-1}(x)$ to get $\Phi(-\Phi^{-1}(x)) = 1 - x \implies -\Phi^{-1}(x) = \Phi^{-1}(1-x)$ – Dhruv Kohli Jul 12 '17 at 17:34
  • Okay, and why $L^2=1$ at the end of the proof? – Cromack Jul 12 '17 at 17:44
  • We proved $L = \frac{1}{L}$. Anything else? – Dhruv Kohli Jul 12 '17 at 17:46
  • Nice proof, thank you! I'd grown fond of the other one, though ;) – Cromack Jul 12 '17 at 17:49
  • Sorry for coming back to the proof. How did you obtain $\frac{\partial\phi(\Phi^{-1}(x))}{\partial x}?$ Isn't it $\frac{\phi^\prime(\Phi^{-1}(x))}{\phi(\Phi^{-1}(x))}$? Then, is $\phi^\prime(\Phi^{-1}(x))=-\Phi^{-1}(x)\phi(\Phi^{-1}(x))$? – Cromack Jul 13 '17 at 07:53
  • Yes. $\phi'(x) = -x\phi(x)$, so $\phi'(f(x)) = -f(x)\phi(f(x))f'(x)$ – Dhruv Kohli Jul 13 '17 at 07:57
  • Sorry for bothering you again. Do you think you can perform the last step ($L^2=1$) taking into account that it's a $\infty / \infty$ indeterminate form? – Cromack Jul 13 '17 at 19:59
  • Yes we can. The form of the limit has nothing to do with that. If $L = \lim_{x\rightarrow 0}\frac{f(x)}{g(x)}$ comes out to be zero or finite non-zero or infinite value then the limit $L' = \lim_{x\rightarrow 0}\frac{g(x)}{f(x)}$ will be $1/L$ and its value will be infinite or finite non-zero or zero. – Dhruv Kohli Jul 13 '17 at 20:10
  • Precisely, you don't know if $\lim_{x\to0}\frac{f(x)}{g(x)}$ comes out to be zero or finite non-zero or infinite value, because there is an $\infty/\infty$ indeterminate form. – Cromack Jul 14 '17 at 06:06
  • Yes. We don't know that. But whatever the value of limit be, the value of $\lim_{x\rightarrow 0} \frac{g(x)}{f(x)}$ will be the inverse of the former value. And I proved that the two values $L$ and $L^{-1}$ are equal. – Dhruv Kohli Jul 14 '17 at 06:09
  • CHeck this https://math.stackexchange.com/questions/939852/the-limit-of-reciprocal-is-the-reciprocal-of-the-limit – Dhruv Kohli Jul 14 '17 at 06:14
  • So, for example, if you had proved that $\lim_{x\to0}\frac{g(x)}{f(x)}=\lim_{x\to0}\frac{f(x)}{f(x)}$, although it is an $\infty/\infty$ indeterminate form ($\lim_{x\to0}f(x)=\infty=\lim_{x\to0}g(x)$), would the result be 1, in that case? – Cromack Jul 14 '17 at 07:42
  • I believe you meant $\frac{f(x)}{g(x)}$ on RHS. Yes the result will be $1$. – Dhruv Kohli Jul 14 '17 at 08:01