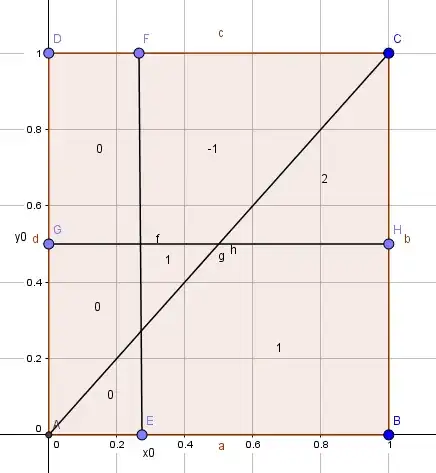
Consider the following game.
You and your opponent is given a uniform random number in the interval $(0,1)$. Player 1 looks at his number and can either bet or fold. If he folds, he loses nothing and the round is over. If he bets and his opponent folds, he wins 1 dollar and the opponent loses nothing. If he bets and his opponent calls, the one with the highest number wins 2 dollars and the loser loses 1 dollar.
So this is an asymmetric game, where player 1 can bet or fold and player 2 can call(if given the chance) or fold. Both players looks at their number before action is taken.
Is this a game of psychology or is there a mathematical way to solve this game? How?
There is only 1 round in this game.
This game is like poker, I was wondering how to assess this situation mathematically? And in isolation.