What is the rigorous definition of a Dirac delta function that evaluates test functions at the boundary of their domain? For example, using spherical coordinates, how do I rigorously interpret the following equation $$\int_0^\infty f(r) \delta(r) d r = f(0)$$ for all test functions $f(r)$ defined for $r \in [0, \infty \rangle$? Equations of this sort are common in physics, but never really justified.
-
2You say "spherical coordinates", but what you describe is not spherical coordinates (which apply to $\Bbb R^3$), but rather a subset of $\Bbb R$. There is a big difference. If $f$ is actually defined on $\Bbb R^3$, but is spherically symmetric so it only depends on the radius, then $f$ is not defined on just $r \in [0,\infty)$. The origin is not a boundary point of $f$, but rather is interior to the domain. The correct integral is $\int_{\Bbb R^3} f(x,y,z)\delta(x,y,z)dV$ – Paul Sinclair Jul 09 '17 at 03:55
-
1@FelixMarin. Another possibility: $\lim_{\epsilon \to 0} \int_0^\infty f(r) , \delta(r-\epsilon) , dr$. – md2perpe Jul 09 '17 at 07:58
-
1@FelixMarin: I think you can take the limit only from above because the function $f(r)$ is not defined for negative $r$. Anyway, I know this is how we physicists deal with radial delta functions, but I was wondering whether they are well define as a Schwartzian distribution/functional. – Jul 09 '17 at 08:17
-
1@PaulSinclair: If $f(x,y,z)$ is spherically symmetric, then we can write $f(x,y,z) = g(\sqrt{x^2 + y^2 + z^2})$ for some function $g(r)$ defined for non-negative $r$. The integral you wrote down reduced to the integral in my question when you perform angular integrations. – Jul 09 '17 at 08:24
-
3But you've missed my point. Which is that $0$ is not a boundary point of the actual test function you are applying the $\delta$ function to. It is only a boundary point of this "reduced version". Which means in this case, you've changed the nature of the problem by this reduction, Instead of treating $f$ as having domain $[0,\infty)$ as a function of $r$, you should treat it as an even function ($f(-x) = f(x)$) on all of $\Bbb R$. – Paul Sinclair Jul 09 '17 at 18:24
-
@PaulSinclair OK, now I get your point. But, if we have a function $f(r)$ which has a nonvanishing derivative at $r=0$, which is a standard situation for radial functions, then the corresponding $f(x)$ in your notation is not a valid test functions since it is not smooth at the origin. – Jul 09 '17 at 20:41
-
2Test functions are required to be smooth. if $f(r)$ has a non-vanishing derivative at the origin, then the function on $\Bbb R^3$ you are trying to represent via radial coordinates is not smooth at the origin and therefore is not a test function. If you can offer one case in physics where such a function is used - and the mathematical model is expected to still hold at that origin, I would be curious to know what it is, because this is a highly non-physical condition. – Paul Sinclair Jul 10 '17 at 16:41
-
In my opinion the integral expression of the OP is incorrect. The reason is that the delta function is symmetric around the origin, and only yields unity when integrated over R. Therefore if you integrate over the positive numbers, the result is half that value. So the right hand side should be: $f(0)/2$. To avoid this inconvenience, it is better to shift the delta function slightly to the right of the origin. That way it is clear that the full delta function is to be evaluated. As suggested above by md2perpe. – M. Wind Jun 14 '20 at 18:47
1 Answers
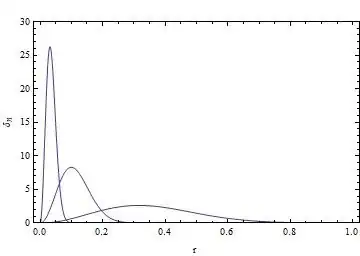
$\def\vr{{\bf r}}$ Consider the integral $$I = \int_{\mathbb{R}^3} g(\vr)\delta(\vr-\vr_0)dV.$$ A standard delta sequence on $\mathbb{R}$ is $$\delta_n(x)=\sqrt{\frac{n}{\pi}}e^{-nx^2}$$ so we write \begin{align*} I_n &= \int_{\mathbb{R}^3} g(r) \left( \prod_{i=1}^3 \sqrt{\frac{n}{\pi}}e^{-n(x_i-x_{i0})^2} \right) dV \\ &= \int_{\mathbb{R}^3} g(r) \left(\frac{n}{\pi}\right)^{3/2} e^{-n(\vr-\vr_0)^2} dV. \end{align*} (By assumption, $g(\vr)=g(r)$.) If $\vr_0={\bf 0}$, then \begin{align*} I_n &= \int_0^{2\pi}\int_0^\pi\int_0^\infty g(r) \left(\frac{n}{\pi}\right)^{3/2} e^{-nr^2} r^2\sin\theta dr d\theta d\phi \\ &= \int_0^\infty g(r) \frac{4n^{3/2}}{\sqrt{\pi}} r^2 e^{-nr^2} dr. \end{align*} Thus, $$\delta_n(r) = \frac{4n^{3/2}}{\sqrt{\pi}} r^2 e^{-nr^2}$$ must be a delta sequence for $\delta(r)$.
Figure 1. $\delta_n(r)$ for $n=10,100,1000$.
- 19,465