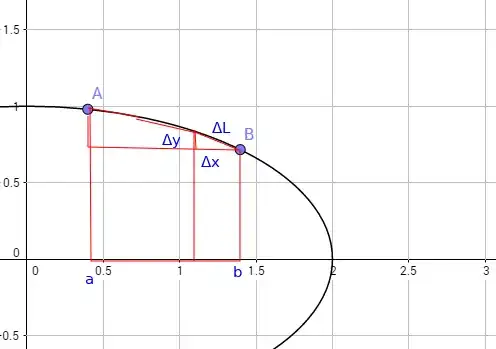
By Pythagoras theorem you have
$$\text{$\Delta $L}=\sqrt{\text{$\Delta $x}^2+\text{$\Delta $y}^2}$$
Collect $\Delta x$ to get
$$ \text{$\Delta $L}=\sqrt{\text{$\Delta $x}^2 \left(\frac{\text{$\Delta $y}^2}{\text{$\Delta $x}^2}+1\right)}=\text{$\Delta $L}=\text{$\Delta $x} \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}$$
Now let $\Delta x\to 0$. If the function is differentiable you get
$${dL}= \sqrt{\left(1+\frac{{dy}}{{dx}}\right)^2}\;{dx}=\sqrt{\left(1+y'\right)^2}\;dx$$
On the interval $[a,b]$ you get
$$L=\int_a^b \sqrt{1+\left(y'\right)^2} \, dx$$
The ellipse on the halfplane where $y>0$ has equation $y=\frac{\sqrt{4-x^2}}{2}$ and its derivative is $y'=-\frac{x}{2 \sqrt{4-x^2}}$ therefore you have
$$L=\int_{0.4}^{1.4} \sqrt{1+\left(-\frac{x}{2 \sqrt{4-x^2}}\right)^2} \, dx=\frac{1}{2} \int_{0.4}^{1.4} \sqrt{\frac{3 x^2-16}{x^2-4}} \, dx$$
This integral is about $L\approx 1.04$ and cannot be calculated with usual functions. That's why the other posters called it "elliptic".
For small intervals, however, it can be approximated by
$$L\approx h \left(1+\frac{1}{2} \left(\frac{b x_0}{a^2}\right)^2\right)$$
where $a$ and $b$ are the parameters of the ellipse, $x_0$ the starting point and $h$ the interval $x_B-x_A$
In your example it gives $L\approx 1.005$ which is a poor approximation, but if you consider $A$ and $B$ closer, let's say $h=0.25$ we get $L\approx 0.251$ while the "exact" formula gives $L\approx 0.252$ which is a fair approximation.
I hope this helps. I preferred a more elementary approach because my intuition suggested you don't eat elliptic integrals for breakfast :)
