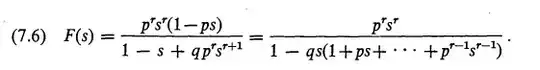I'm trying to solve a problem regarding the probability that a success run of at least length 2 for an event with a probability of 0.8 occurs at least once within n number of trials. I found the following Stack Exchange question which details a formula (see second link) to approximate this probability: Probability of 20 consecutive success in 100 runs. However, when I input 0.8 as my probability and 2 as my run length, the formula returns a value that says the probability of no run occurring is 0, which is obviously false. Am I computing the probability wrong? Or is the formula flawed?
Asked
Active
Viewed 1,087 times
2
-
To add, my n-value is 82. – Justin Borromeo Jul 06 '17 at 21:57
1 Answers
1
There is a little interesting issue with the formula in the linked question.
Feller says (p 324,. XIII.7) that
the second representation in (7.6) shows clearly that the denominator has a unique positive root $s=x$
(emphasis mine)
Then he defines $x$ as the root of $V(x)=0$, where $V(s)=1-s+qp^r s^{r+1}$. But this is the denominator of the first fraction (not of the "second representation"!). And it's not longer true that this denominator has one root, there is one extra root (with respect to the second one), given by $s=1/p$.
Hence Feller is being a little sloppy here. The correct recipe to find $x$ is: find the positive roots of $V(s)$, which will be two, and discard the root $1/p$; the other one is $x$.
In your case, $V(r)$ has the roots $\{1.25,1.951941\}$. Hence $x=1.951941$
(Notice that the "good" root can be less or greater that the "spurious" one. For example, for $p=0.6$ we get $\{1.37146,1.66666\}$, the good is the first one)
I'll edit the other answer to clarify this.
leonbloy
- 63,430
-
-
I think you are misreading Feller here: he defines $x$ as the unique positive root of $1-qs(1+ps+\cdots+p^{r-1}s^{r-1})$, not $V(s)$. He later uses that fact that $x$ is also a root of $V$, but that is not its definition. – Sep 13 '17 at 13:43