3

enter image description here

The volume of the object in the above picture is given by, $$V=\int_{0}^{4} \pi y^2dx$$

While dealing with calculating surface areas of objects, I was introduced to the integral, $$S=\int_{0}^{4} 2\pi y\sqrt{1+(y')^2} dx$$ where $\sqrt{1+(y')^2} dx$ is the infinitesimal arc length.

Is it reasonable to improve the definition of the volume of a solid object to be $V=\int_{0}^{4} \pi y^2\sqrt{1+(y')^2} dx$?

enter image description here

Geometrically, the segment length is a better approximation. However, when the interval tends to zero, the arc, segment and $\Delta x$ tend to coincide. So, as the interval goes to zero, I can consider the infinitesimal segment length instead of $dx$, can I not?

What I would like to know is if $V=\int_{0}^{4} \pi y^2\sqrt{1+(y')^2} dx$ is valid or not. If not, then why?

R004
  • 983
  • 2
    Aren't your two $V$s not equal? So no? – Shuri2060 Jul 06 '17 at 12:55
  • Compute the volume of the circular cylinder obtained by rotating the line $y=1$ around the $x$ axis and bounded by $x=0$ and $x=1$. Then compute the volume of the union of the same cylinder but bounded by $x=1/n$ and $x=1$ with the cone generated by revolving $y=nx$ around the $x$ axis and bounded between $x=0$ and $x=1/n$. Take the limit as $n\to\infty$. – Bettybel Jul 06 '17 at 13:09
  • The volume of the shown paraboloid is not $\int_{0}^{4}\pi y^2,dy$ but $$ V=\int_{0}^{4} \pi x,dx = \color{red}{8\pi}$$ since the section $x=k$, for any $k\in[0,4]$, is a circle having area $\pi x$. – Jack D'Aurizio Jul 06 '17 at 14:34
  • The surface area is given by $$ \int_{0}^{4}2\pi g(x)\sqrt{1+g'(x)^2},dx $$ where $g(x)=\sqrt{x}$ (see here: http://tutorial.math.lamar.edu/Classes/CalcII/SurfaceArea.aspx) hence $$ S = \int_{0}^{4}2\pi \sqrt{x+\frac{1}{4}},dx =\color{red}{\frac{\pi}{6}\left(17\sqrt{17}-1\right)}.$$ – Jack D'Aurizio Jul 06 '17 at 14:38
  • Jack, I believe you mistyped. I did state that the volume was $\int_{0}^{4} \pi y^2 dx$. I am aware of the concept of evaluating Surface areas. If you look closely, I am asking for something else. – R004 Jul 06 '17 at 17:47
  • You should see this answer https://math.stackexchange.com/a/1692595/72031 – Paramanand Singh Jul 07 '17 at 07:18
  • Also how do you get the volume of the slice between $x$ and $x+dx$ as $\pi y^{2}\sqrt{1+y'^{2}},dx$? We can't arbitrarily use any formula. A slice of such a solid is almost like a frustum of a cone and you should try to use the formula for volume as well as surface area of a frustum and you will get things as expected. – Paramanand Singh Jul 07 '17 at 07:28
  • Yes. In the comments to a post, I corrected myself. – R004 Jul 07 '17 at 07:42

2 Answers2

1

This is perhaps best explained in terms of Pappus's Centroid Theorems:

Pappus's $(1^{st})$ Centroid Theorem states that the surface area $A$ of a surface of revolution generated by rotating a plane curve $C$ about an axis external to $C$and on the same plane is equal to the product of the arc length $s$ of $C$ and the distance d traveled by its geometric centroid (Pappus's centroid theorem). Simply put, $S=2\pi RL$, where $R$ is the normal distance of the centroid to the axis of revolution and $L$ is curve length. The centroid of a curve is given by

$$\mathbf{R}=\frac{\int \mathbf{r}ds}{\int ds}=\frac{1}{L} \int \mathbf{r}ds$$

Pappus's $(2^{nd})$ Centroid Theorem says the volume of a planar area of revolution is the product of the area $A$ and the length of the path traced by its centroid $R$, i.e., $2πR$. The bottom line is that the volume is given simply by $V=2πRA$. The centroid of a volume is given by

$$\mathbf{R}=\frac{\int_A \mathbf{r}dA}{\int_A dA}=\frac{1}{A} \int_A \mathbf{r}dA$$

Thus we can say for your cases that

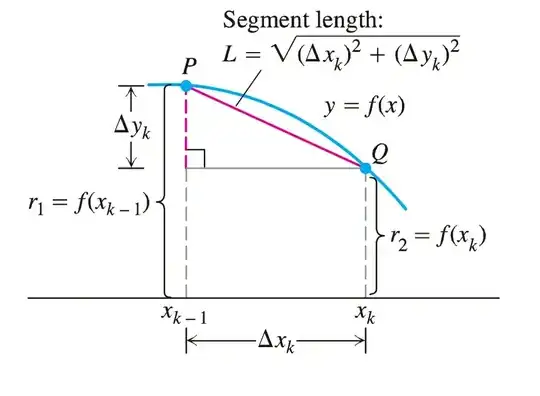
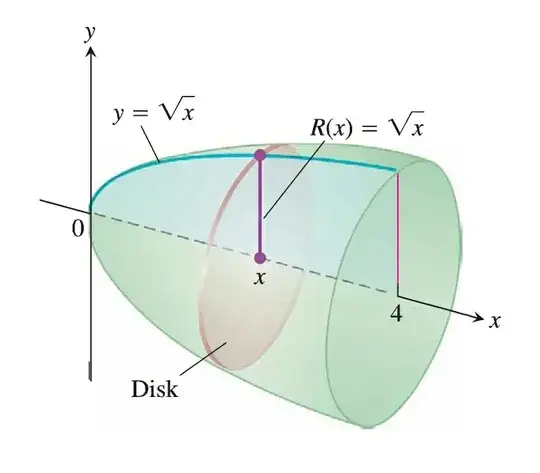
$$ S=2\pi\int_0^4 y\ ds =2\pi\int_0^4 y\sqrt{1+y'^2} dx\\ V=\pi\int_0^4 y^2\ dx $$

This is just as stated in the OP. Notice that here, the length, $L$ and the volume, $V$ have cancelled out, thus disguising the true nature of the equations.

Now, clearly you can't have

$$V=\pi\int_0^4 y^2\ dx=\pi\int_0^4 y^2\sqrt{1+y'^2} ~dx$$

But more to the point, the volume pertains to the area under the curve, whereas, the term $\sqrt{1+y'^2}$ in the surface area equation refers to the area along the arc of $ds$ and it has nothing to do with the volume of revolution.

Cye Waldman
  • 7,524
  • The geometry seems to confuse me. The segment length appears to be a better approximation than $\Delta x$. As the interval falls to zero, the segment length and $\Delta x$ fall on each other. The difference in lengths becomes insignificant. However, replacing $dx$ with the infinitesimal segment length does not yield the right result. The geometry suggests whereas the math does not. – R004 Jul 07 '17 at 02:27
  • Oh! Wait a minute. I realized where I went wrong. My integrand was a product of the slant height of a frustum and the area of a circle. This is wrong because the volume of a cylinder is not the mentioned product. Ah! Silly mistake. – R004 Jul 07 '17 at 03:23
  • This brings me to another question. Can I calculate the volume of a solid by integrating infinitesimal frustum volumes? The reason why I asked this is because in wiggly, non-cylindrical solids, a frustum is a better approximation than a cylinder. Well, as $\Delta x$ goes to zero, the frustum and the cylinder become identical. I'm not sure if integrating frustum volumes will give us better results. But I am sure that the process will become complicated. – R004 Jul 07 '17 at 03:29
  • Pardon the long wait, we must be in different time zones. Okay, I think you've got the idea. Think in terms of the area, we all know that area is the integral of $y(x)~dx$. But really, it's the integral of $dA=dy~dx$. That is, the differential area is the the rectangle $dy~dx$. If you were to use the differential area as the frustum, you would be incorrect over almost the entire area. – Cye Waldman Jul 07 '17 at 14:44
  • Here, Paramanand Singh has reasoned why we can use differential frustum volumes. – R004 Jul 07 '17 at 14:55
  • 1
    I haven't the time to replicate what he has done, but he's has not demonstrated that the integral over $dx$ is the same as that over $ds$. It looks pretty sophisticated but you are better off sticking with the well-established mathematics. As for myself, I never think in in terms of discs and washers, but always use Pappus's theorems which are easy to remember and foolproof. – Cye Waldman Jul 07 '17 at 15:06
  • I believe that Pappus's theorem is convenient to use when dealing with surfaces and arcs of known length. In the case of wiggly surface and arcs, I think it gets complicated. Nonetheless, it works. – R004 Jul 07 '17 at 15:27
  • 1
    It doesn't matter, you absolutely must end up with the same integral; it's just a matter of how you get there-and with what certainty. – Cye Waldman Jul 07 '17 at 15:47
0

It is reasonable to improve the definition of the volume of a solid object that can be defined to be

$$V=\int_{0}^{4} \pi y^2 dx$$

by assembly of infinitesimally thin disks shown, so that the direction of building up of volume is strictly perpendicular to the base circle plane.

( Surface area of the solid is obtained by assembling lateral areas of connected cones).

Narasimham
  • 40,495