I'd like to come up with a probabilistic argument to evaluate the following limit: $$\lim_{n\to\infty} e^{-n} \sum_{k = 0}^n \frac{n^k}{k!}$$
The reason is that, if $X \sim \mathrm{Poisson}(n)$, the limit translates to $$\lim_{n\to\infty} F_X(n)$$ where $F_X$ is the cumulative distribution function of $X$. I know that it can be expressed by resorting to the gamma function and its incomplete counterpart, but I don't think I'll be able to evaluate the limit if I substitute that expression.
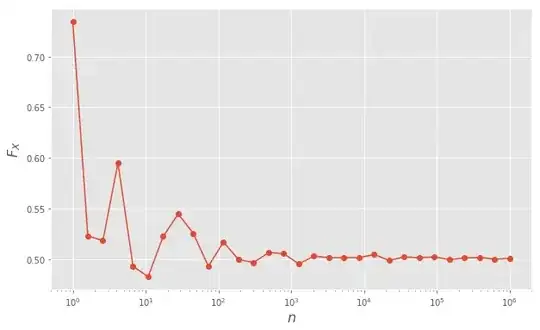
Is there a simpler probabilistic argument in this case? In the meantime, I confirmed the limit indeed exists, and it's $1/2$:
import scipy as sp, matplotlib.pyplot as plt
F_X = lambda n: (sp.stats.distributions.poisson.rvs(n, size=100000) <= n).mean()
ns = np.logspace(0, 6, 30)
fig, ax = plt.subplots(figsize=(10, 6))
ax.semilogx(ns, list(map(F_X, ns)), marker='o')
ax.set_xlabel('$n$', fontsize=16)
ax.set_ylabel('$F_X$', fontsize=16)