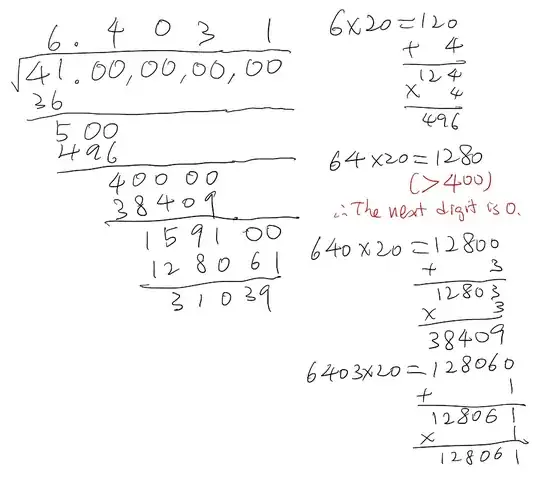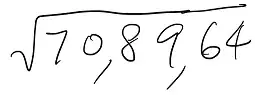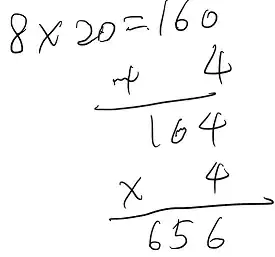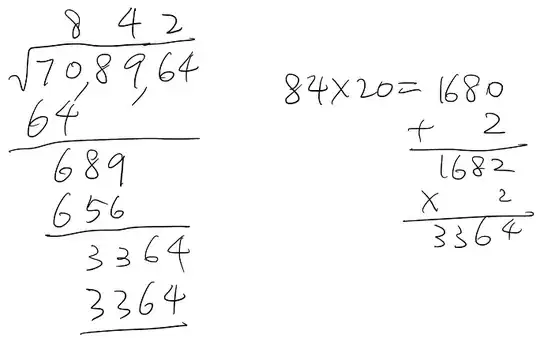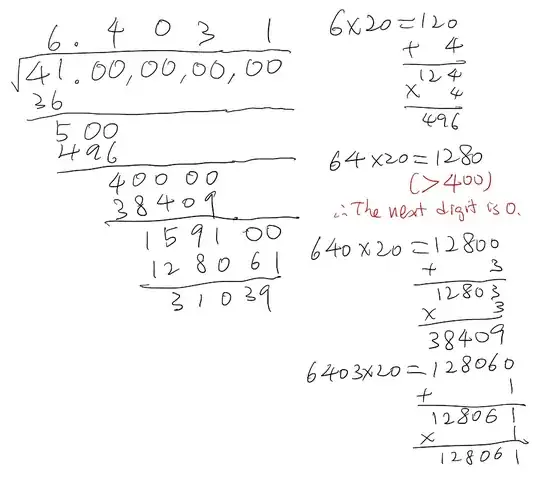2

Evaluate $\sqrt{41}$ to $n$ decimal places without using a calculator.

$$x^2 -10x-16=0$$ I was asked to solve the above quadratic giving the solutions to one decimal place.

Using the quadratic formula I got: $x= 5\pm \sqrt{41}$

Using a calculator that is: $11.4(1dp)$ or $-1.4(1dp)$

Then I wondered if I could solve this without a calculator.

It can be done by trial and error squaring values and gradually getting closer to the required accuracy. Here are the values that I squared to get to the required accuracy for the above case. $6.5,6.4,6.45,6.43,6.41$ and $6.405$. But is there another cleaner way of solving a surd to some number of decimal places?

Kantura
  • 2,721

7 Answers7

2

Hint. Construct a recurrence sequence $x_n=f(x_{n-1})$ for $n\geq 1$, with $$f(x)=\frac{1}{2}\left(x+\frac{41}{x}\right).$$ A reasonable starting point would be $x_0=7$ (note that $6^2<41<7^2$). For details take a look here.

Robert Z
  • 145,942
2

Well, $42=6\cdot7$, so $6.5^2=42.25$, meaning $\sqrt{41}=\sqrt{42.25-1.25}\approx6.5-\frac{1.25}{2\cdot6.5}\approx6.4$. It's not really different from the other answer, the first step of Newton method, essentially, with $x_0=6.5$.

2

There is a method to find the square root of a number. It looks just like long division.

The method is based on the identity $(10a+b)^2=100a^2+(20a+b)b$.

I am not native in English and have some difficulties to describe the method clearly. Hope the pictures help.

Take $708964$ as an example.

Step 1: divide the digits into groups of two, starting from the decimal point. (The leftmost group is $70$.)

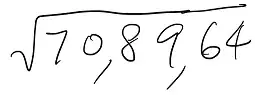
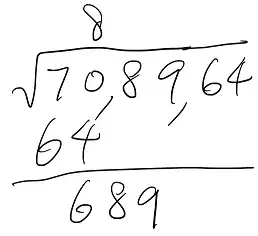
enter image description here

Step 2: find the largest integer which is not larger than the square root of the first group. Subtract its square from the first group. Copy the second group right after the difference. (The first digit of the answer is $8$.)

enter image description here

Step 3: multiply the number on the top row by $20$. ($8\times 20=160$)

enter image description here

Step 4: the next digit of the answer is approximately equal to the quotient when the number in Step 2 divided by the number in Step 3. ($689\div160$ gives $4$). Add this to the number in Step 3. Then multiply the sum by this guess. ($(160+4)\times 4=656$) [Note: if this product is larger than the number in Step 2, reduce the guess by $1$ and do it again.

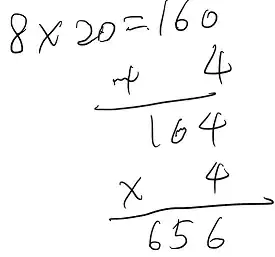
enter image description here

Step 5: write the number obtained in Step 4 right below the number in Step 2. Do the subtraction. Copy the third group after the difference. Write the guess of the second digit in Step 4 on the top row after the first digit. It is the second digit of the square root.

enter image description here

Step 6: Repeat the process starting from Step3, but replace the first digit by the two-digit number now on the top row. Work recursively until the remainder is $0$, or up to the desired number of significant figures.

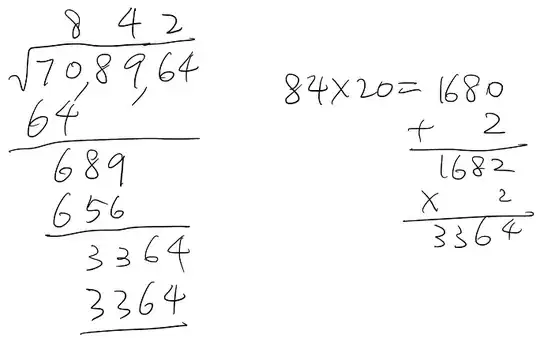
enter image description here

Below is how I compute the square root of $41$ up to $4$ digits after the decimal point.

enter image description here

CY Aries
  • 23,393
  • You do not like to use LaTeX, oder..? – Darío A. Gutiérrez Jun 06 '17 at 20:41
  • @DaríoA.Gutiérrez, I am inclined to be tolerant of non-TeX here, since I myself would not know immediately how to achieve the relevant formatting! :) – paul garrett Jun 08 '17 at 21:54
  • Yes, aeons ago, before widely accessible calculators, much less computers of any kind, I learned this method. Note that it is a fairly optimized version of a guess-and-check algorithm to obtain successive digits. – paul garrett Jun 08 '17 at 21:56
1

The square root of a prime number $41$ is always irrational.
However you can calculate an approximation of $\sqrt{41}$

We know $$\sqrt{36}<\sqrt{41}<\sqrt{49}$$ $$6<\sqrt{41}<7$$ therefore $\sqrt{41} \simeq 6,...$
You can approximate the decimal value as follows:

$$41 - 36 = 5 \text{ and } 2\cdot 6= 12$$ Also..

$$\sqrt{41} \simeq 6 + \frac{5}{12} = 6.4$$

Here you can see another method with an example on $\sqrt{45}$

Darío A. Gutiérrez
  • 3,863
1

For $x=5+\sqrt{41}$, $$x^2-10x-16=0$$ $$x^2=10x+16$$ $$x=10+\cfrac{16}{x}$$ Now, put $x=5+\sqrt{41}$ back again, $$\begin{align}\sqrt{41}&=5+\cfrac{16}{5+\sqrt{41}}\\ &=5+\cfrac{16}{10+\cfrac{16}{5+\sqrt{41}}} \\ &=5+\cfrac{16}{10+\cfrac{16}{10+\cfrac{16}{10+\cfrac{16}{10+\cfrac{16}{5+\sqrt{41}}}}}}\label{1}\tag{*} \end{align}$$ And actually, we have $$\sqrt{41}=5+\cfrac{16}{10+\cfrac{16}{10+\cfrac{16}{10+\ddots}}}$$ Which could be used in the approximation, I think. For a partial numerical answer, it should be good to put the $\sqrt{41}$ on the $R.H.S.$ to be $6$ and $7$ at $(\ref{1})$ respectively, well, maybe up to a higher continuous fraction degree, when the gap between them is to be sufficiently small, then the approximation could be valid.

BAI
  • 2,565
1

The continued fraction convergents are alternately slightly above and slightly below $\sqrt {41}.$ $$ \frac{ 32 }{ 5 } < \sqrt {41} < \frac{ 397 }{ 62 } $$

Method described by Prof. Lubin at Continued fraction of $\sqrt{67} - 4$

$$ \sqrt { 41} = 6 + \frac{ \sqrt {41} - 6 }{ 1 } $$ $$ \frac{ 1 }{ \sqrt {41} - 6 } = \frac{ \sqrt {41} + 6 }{5 } = 2 + \frac{ \sqrt {41} - 4 }{5 } $$ $$ \frac{ 5 }{ \sqrt {41} - 4 } = \frac{ \sqrt {41} + 4 }{5 } = 2 + \frac{ \sqrt {41} - 6 }{5 } $$ $$ \frac{ 5 }{ \sqrt {41} - 6 } = \frac{ \sqrt {41} + 6 }{1 } = 12 + \frac{ \sqrt {41} - 6 }{1 } $$

Simple continued fraction tableau:
$$ \begin{array}{cccccccccccccccc} & & 6 & & 2 & & 2 & & 12 & & 2 & & 2 & & 12 & \\ \\ \frac{ 0 }{ 1 } & \frac{ 1 }{ 0 } & & \frac{ 6 }{ 1 } & & \frac{ 13 }{ 2 } & & \frac{ 32 }{ 5 } & & \frac{ 397 }{ 62 } & & \frac{ 826 }{ 129 } & & \frac{ 2049 }{ 320 } \\ \\ & 1 & & -5 & & 5 & & -1 & & 5 & & -5 & & 1 \end{array} $$

$$ \begin{array}{cccc} \frac{ 1 }{ 0 } & 1^2 - 41 \cdot 0^2 = 1 & \mbox{digit} & 6 \\ \frac{ 6 }{ 1 } & 6^2 - 41 \cdot 1^2 = -5 & \mbox{digit} & 2 \\ \frac{ 13 }{ 2 } & 13^2 - 41 \cdot 2^2 = 5 & \mbox{digit} & 2 \\ \frac{ 32 }{ 5 } & 32^2 - 41 \cdot 5^2 = -1 & \mbox{digit} & 12 \\ \frac{ 397 }{ 62 } & 397^2 - 41 \cdot 62^2 = 5 & \mbox{digit} & 2 \\ \frac{ 826 }{ 129 } & 826^2 - 41 \cdot 129^2 = -5 & \mbox{digit} & 2 \\ \frac{ 2049 }{ 320 } & 2049^2 - 41 \cdot 320^2 = 1 & \mbox{digit} & 12 \\ \end{array} $$

Will Jagy
  • 139,541
1

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} \root{41} & = \sqrt{4100 \over 100} = {1 \over 10}\root{4096 + 4} = {32 \over 5} \root{1 + {1 \over 1024}} \\[5mm] & = {32 \over 5}\bracks{1 + {1/2 \over 1024} - {1/8 \over 1024^{2}} + \cdots} = {32 \over 5}\sum_{k = 0}^{\infty}{{1/2 \choose k} \over 1024^{k}} \end{align}

The following table shows the 'truncated expression' $\ds{{32 \over 5}\sum_{k = 0}^{\color{#00f}{\Large n}}{{1/2 \choose k} \over 1024^{k}}}$: $$ \begin{array}{rl}\hline \ds{\color{#00f}{\Large n}} & \ds{6.403124237432848686488217674621813264520\ldots = \root{41}} \\ \hline \ds{0} & \ds{6.4} \\ \ds{1} & \ds{6.40312\color{#f00}{5}} \\ \ds{2} & \ds{6.403124237\color{#f00}{060546875}} \\ \ds{3} & \ds{6.40312423743\color{#f00}{307590484619140625}} \\ \ds{4} & \ds{6.403124237432848\color{#f00}{5311707481741905212402344}} \\ \ds{5} & \ds{6.403124237432848686\color{#f00}{6019716217124368995428}} \\ \ds{6} & \ds{6.403124237432848686488\color{#f00}{1303936014589339720}} \end{array} $$

It converges very fast. Even the third term

$$ \pars{~n = 2 \implies {8392703 \over 1310720} = 6.403124237\color{#f00}{060546875}~}\ \mbox{yields}\ \color{#00f}{\large 9}\ \mbox{exact decimals !!!}. $$

Felix Marin
  • 89,464