2

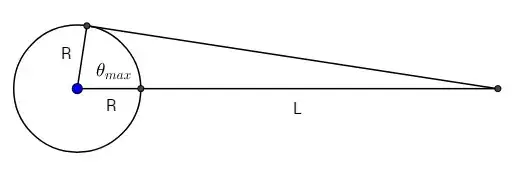
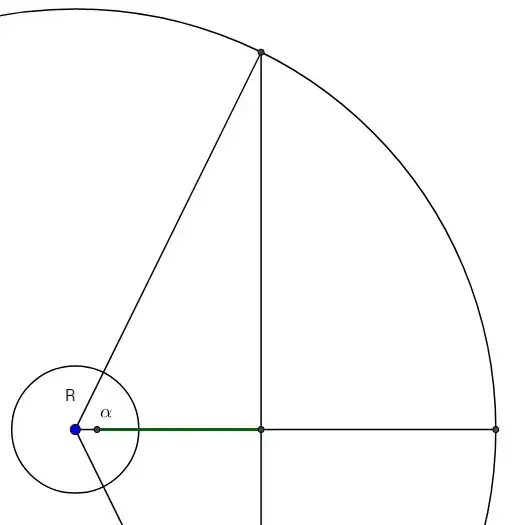
The Clarke Belt of geostationary satellites cannot be seen from the ground above latitude 81.38 degrees. (At that latitude, an earth station can only see a satellite directly on its own line of longitude.) So the belt is 5.67 times the radius of the earth in altitude ($\sec(81.38) -1$).

At the other extreme (on the equator), an earth station can see about 162.8 degrees of the Clarke Belt ($2 * 81.38$).

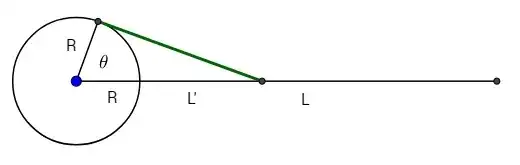
Calculations of the portion of the belt visible from intermediate latitudes would be a three-dimensional trig problem calculated from the intersection of the plane tangent to the earth station's position with the Clarke Belt.

I'd love some help with that problem. Obviously, all answers would be between 0 and 162.8 degrees. Thanks.

N. Joseph Potts
  • 31

1 Answers1

2

You don't actually need 3D trig to solve this.

enter image description here

Above is a sketch of the Earth seen from the side, with the North Pole on top. $R$ is the radius of the Earth, $L$ is the distance from the Earth's surface to the Clarke Belt and $\theta_{max}$ is the maximum latitude where the belt is visible. We see that $$\cos \theta_{max} = \frac{R}{R+L}\tag {1}$$ If you select some latitude $\theta \lt \theta_{max}$ you will have the situation below:

enter image description here

The tangent to the Earth at this latitude will intersect the segment $L$ at some shorter distance $L'$ above the Earth. We see that: $$\cos \theta = \frac{R}{R+L'}\tag{2}$$

Looking at the above situation from the North Pole, we get the figure below:

enter image description here

From this figure we see that $$\cos \alpha = \frac{R+L'}{R+L}\tag{3}$$ Combining equations $1$ and $2$ with $3$ we find that $$\alpha = \arccos(\frac{\cos \theta_{max}}{\cos \theta})$$

Jens
  • 5,686
  • 2
  • 20
  • 38
  • Thank you AGAIN, Jens. I think you forgot to multiply $\alpha$ by 2. My own solution was (like yours) $2*\arccos(\sec(\frac{latitude}{\sec(81.38)}))$. I think that works out to the same thing, except for my coefficient. And you're right: no 3D trig needed. – N. Joseph Potts Jun 06 '17 at 20:29
  • Formula in my comment is wrong. Should be $2*\arccos(\frac{\sec(latitude}{\sec(81.38)}))$. It's going to be a long time before I get much good at this. – N. Joseph Potts Jun 06 '17 at 20:37