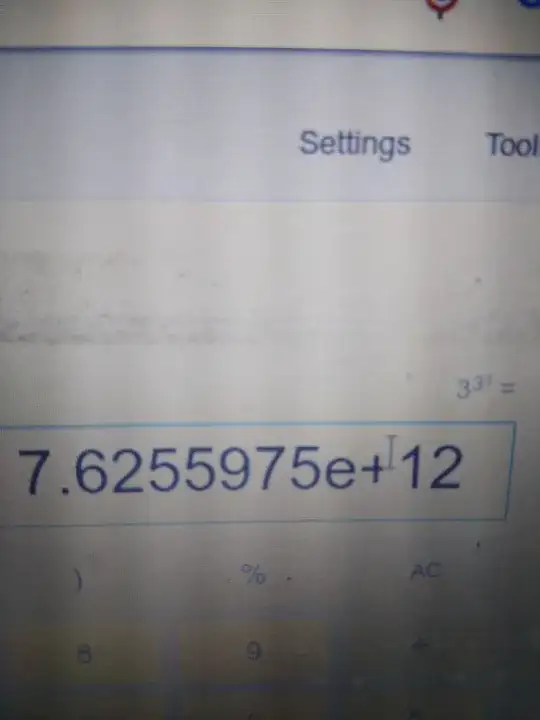
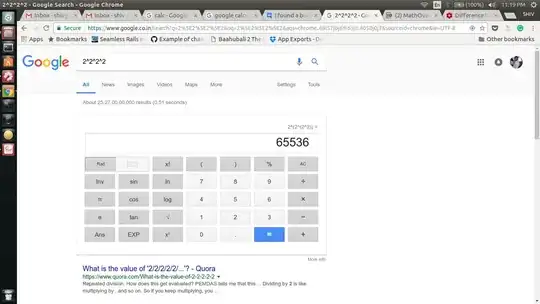
I tried to compute the power of 2^2^2^2 on google calculator and my casio calculator but both are giving different results. same is true for 3^3^3. Please explain me the difference between two expressions.
2 Answers
Your calculator is interpreting it as this:
$${{2^2}^2}^2 = ((2^2)^2)^2 = (4^2)^2 = 16^2 = 256$$
Google is interpreting it as this:
$${{2^2}^2}^2 = 2^{(2^{(2^2)})} = 2^{(2^4)} = 2^{16} = 65536$$
Similarly with the threes.
Technically Google is correct because order of operations says to do exponents first. So when we want to evaluate $2^{\color{red}{2}^{\color{blue}{2^2}}}$, order of operations says to evaluate the $\color{red}{{2^{\color{blue}{2^2}}}}$ first, i.e., evaluate the exponent first. Apply this rule again and it tells us we're supposed to evaluate the $\color{blue}{2^2}$ first, which is $4.$ Therefore $\color{red}{{2^{\color{blue}{2^2}}}} = 2^4 = 16$, and so $2^{\color{red}{2}^{\color{blue}{2^2}}} = 2^{16} = 65536$.
-
What is correct mathematically? – shiv garg Jun 02 '17 at 18:05
-
1@shivgarg, technically Google is correct because order of operations says to do exponents first. Also see my edit in my answer. – Jun 02 '17 at 18:08
-
"what is correct mathematically?" is also answered in greater detail in the linked question that you should see a link to above, but here it is again in case you missed it. – JMoravitz Jun 02 '17 at 18:09
-
In cases like this it never hurts to be explicit about the order you intend. Use parens to instruct Google (or a more modern calculator) how you want it processed. – SDsolar Jun 02 '17 at 18:13
-
Actually, I don't think there is a "correct" answer. It's a matter of convention, and the convention is not set in stone. – Robert Israel Jun 02 '17 at 18:14
-
@RobertIsrael So if you instructed your students to evaluate $2^{2^2}$, would you mark them off if they did it one way or the other? Oh, wait ... :) – John Jun 02 '17 at 19:19
The difference lies in the applied order of operations.
The Casio calculator does operations strictly left to right unless you break it with parentheses:
2^2^2^2 = 4^2^2 = 16^2 = 256
But Google evaluates the entire expression (correctly) using right-to-left order or operations for the stacked powers:
2^2^2^2 = 2^2^4 = 2^16 = 65536
- 26,319