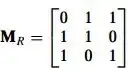What you want is not the inverse of the matrix $M_R$, but rather the matrix of the inverse relation $R^{-1}$: you want $M_{R^{-1}}$, not $(M_R)^{-1}$. Elementary row operations are one way of computing$(M_R)^{-1}$, when it exists, they won’t give you $M_{R^{-1}}$.
Note also that while $(M_R)^{-1}$ doesn’t always exist: The relation $R=\{\langle 1,2\rangle\}$ on $\{1,2\}$ has the matrix $$M_R=\begin{bmatrix}0&1\\0&0\end{bmatrix}\;,$$ and you can easily check that this $M_R$ is not invertible in the linear algebra sense.
Every relation, however, has an inverse relation, so for any relation $R$, $M_{R^{-1}}$ exists. Recall that if $R$ is a relation on $A$, $$R^{-1}=\Big\{\langle y,x\rangle\in A\times A:\langle x,y\rangle\in R\Big\}\;:$$ it’s the relation that you get from $R$ by ‘turning all the ordered pairs around’. This operation actually does have an effect on the matrix that is familiar from linear algebra, but it’s not taking the inverse of the matrix: it’s taking the transpose. For example, if $R=\{\langle 1,2\rangle\}$ on $\{1,2\}$, $R^{-1}=\{\langle 2,1\rangle\}$, and
$$M_{R^{-1}}=\begin{bmatrix}0&0\\1&0\end{bmatrix}=\begin{bmatrix}0&1\\0&0\end{bmatrix}^T=M_R^T\;.$$
For any relation $R$, the rows of $M_R$ correspond to the first components of the ordered pairs in $R$, and the columns of $M_R$ correspond to the second components. When you turn the pairs around to form $R^{-1}$, you interchange the first and second components, and this has the effect of interchanging the rows and columns of the matrix. But that’s exactly what transposing does, so you automatically get $M_{R^{-1}}=M_R^T$.
This is nice, actually, since it’s easier to find the transpose of a matrix than it is to find the inverse, even when it exists!