Speechless mathematical proofs.

Question

Do you have proofs without word?

Your proofs are not necessary has zero word, you may add a bit explanations.

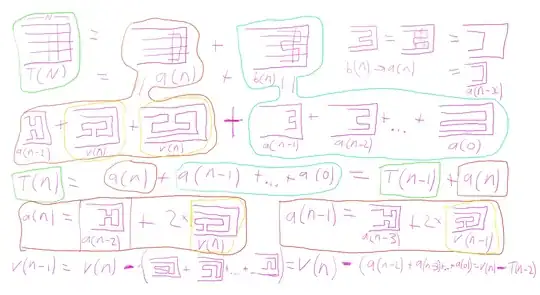
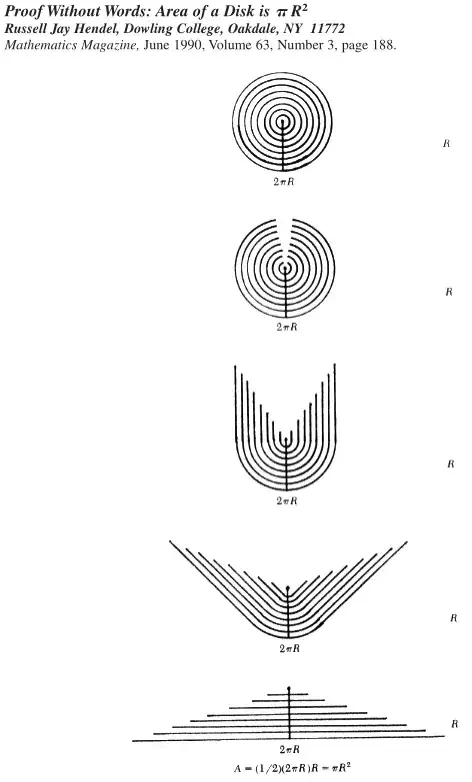
As an example, I has a "Speechless proof" for $$\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+...=\frac{1}{3}$$ enter image description here

I welcome all aspects of mathematical proofs. Thank you.

These are usually called proofs without words. MathOverflow has a nice list of them. — , Nov 05 '12 at 09:05
Please feel please to post your proof even it's similar to those in MathsOverFlow, because we are here in MathStackExchange. — JSCB, Nov 05 '12 at 09:58
(-1) There is already some many lists of proof without words... It is not a very imaginative question. At least it, should be community wiki. — Lierre, Nov 05 '12 at 10:19
For this question, what's really important are imaginative answers. — JSCB, Nov 05 '12 at 10:27
In fact, this particular example is not obvious without some words (at least to me)! — NoChance, Nov 05 '12 at 10:40
@NoChance, you are right. Also, there is a nice proof without words for the same result here: (https://mathoverflow.net/a/163807). This is in the list mentioned in the comment above by Rahul. — Cyriac Antony, Jan 17 '19 at 05:14
Does this answer your question? Visually stunning math concepts which are easy to explain — user95921, Dec 26 '23 at 06:44

score 8 · Answer 1 · 2012-11-05T09:22:20.300

8

The best one I have ever seen is to prove $$1 + 2 + 3 + \cdots + n = \dfrac{n(n+1)}2$$

enter image description here

edited Nov 05 '12 at 09:22

answered Nov 05 '12 at 09:16

1

Should we just copy the MO answers here - or link to them from here? – Old John Nov 05 '12 at 09:50
2

Could somebody give me the "with words" version of this proof? – littleO Nov 05 '12 at 10:05
3

@littleO There's a bijection in there. Look carefully. Perhaps it would be more helpful if we wrote $\frac{n(n+1)}{2}$ as $\binom{n+1}{2}$ – EuYu Nov 05 '12 at 10:09
Ohh, I see, crazy. Thanks for the hint. – littleO Nov 05 '12 at 12:00
@OldJohn I don't know. I anyway made my post CW when I posted it. – Nov 05 '12 at 21:48

score 8 · Answer 2 · edited Apr 08 '20 at 22:25

8

Found this great one surfing the web recently. $$ \displaystyle \huge \frac12+\frac14+\frac18+\frac1{16}+\frac1{32}+\ldots =1 $$ Classic geometric sum

edited Apr 08 '20 at 22:25

Khosrotash

24,922

answered Nov 05 '12 at 09:49

cyclochaotic

1,355

score 6 · Answer 3 · answered Nov 05 '12 at 10:16

6

Convergence of reciprocal of squares

Reciprocals of squares converge.

answered Nov 05 '12 at 10:16

EuYu

41,421

score 0 · Accepted Answer · answered Nov 05 '12 at 09:54

Part of the proof in my blog post is done with my own ad-hoc diagrams..

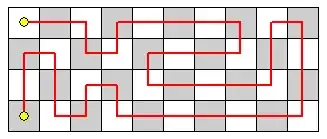
grid with tour

The question is: How many "tours" (paths that visit every single square exactly once) are there in a 4x10^12 grid under the condition the tour must start in the top left square and finish in the bottom left square. (Credit to the guys at projecteuler.net for thinking up another great problem)

If we let T(n) be the formula for the number of tours in a 4xn grid, we need to find T(10^12). One approach is to find a recurrence relation. A trick is to realize there are only two possible ending columns. Try follow my working if you can, sorry It's messy :)

sketch

score 0 · Answer 5 · answered Apr 16 '18 at 16:42

0

Here's one showing the area of a disk is $\pi R^2$.

answered Apr 16 '18 at 16:42

Charles

195
1
8

This happens to end with the correct answer, but the method is invalid, because it assumes that $\lim_{n\to\infty} a(n)=a(\infty)$ where $a(n)$ is the total area of the $n$ strips after division into $n$ parts, and $a(\infty)$ is the circle's area. – Rosie F May 15 '19 at 19:05

Speechless mathematical proofs.

5 Answers5

Linked