Evaluating closed form of $I_n=\int_0^{\pi/2} \underbrace{\cos(\cos(\dots(\cos}_{n \text{ times}}(x))\dots))~dx$ for all $n\in \mathbb{N}$.

Question

I was wondering if there is any way to evaluate a general closed form solution to the following integral for all $n\in \mathbb{N}$. $$I_n=\int_0^{\pi/2} \underbrace{\cos(\cos(\cos(\dots(\cos}_{n \text{ times}}(x))\dots)))~dx \tag{1}$$

I have already evaluated closed forms to this integral for certain values of $n$, however I am still missing a closed form for a large number of values of $n$. Those in $\color{red}{\text{red}}$ I numerically evaluated, meaning that I currently do not have a closed form for them. $$\begin{array}{c|c}n&I_n\\\hline0&\dfrac{\pi^2}{8}\\1&1\\2&\dfrac{\pi J_0(1)}{2}\\\color{red}{3}&\color{red}{\approx 1.11805}\\\color{red}{4}&\color{red}{\approx 1.18186} \\ \color{red}{5} & \color{red}{\approx 1.14376} \\ \color{red}{6}&\color{red}{\approx 1.17102}\\\color{red}{\vdots}&\color{red}{\vdots}\\\infty&\alpha\cdot \dfrac{\pi}{2} \approx 1.16095\end{array}$$ Where $J_p(\cdot )$ is the Bessel function of the first kind, and $\alpha$ is the Dottie Number. The cases $n=0$ and $n=1$ are trivial, hence I will not show how I derived these solutions. Hence, I will show how I derived the case where $n=2$ and $n\to \infty$.

---

Evaluating $I_2$: i.e $\int_0^{\pi/2} \cos(\cos(x))~dx$.

Introducing the definition of the Bessel Function of the first kind: $$J_{\beta}(z)=\frac{1}{\pi}\int_0^{\pi} \cos(z\sin{\theta}-\beta \theta)~d\theta$$ We can use the substitution $\theta=u+\frac{\pi}{2}$ to obtain:

$$\begin{align} J_{\beta}(z)&=\frac{1}{\pi}\int_{-\pi/2}^{\pi/2} \cos\left(z\sin\left(u+\frac{\pi}{2}\right)-\beta\left(u+\frac{\pi}{2}\right)\right)~du\\&=\frac{1}{\pi}\int_{-\pi/2}^{\pi/2} \cos\left(z\cos(u)-\beta\left(u+\frac{\pi}{2}\right)\right)~du \end{align}$$ To get it into a similar form to our case, notice that we can let $\beta=0$ and $z=1$. Therefore: $$J_0(1)=\frac{1}{\pi}\int_{-\pi/2}^{\pi/2} \cos(\cos(u))~du$$ At first sight, it may seem like the bounds are problematic. However, note that $f(x)=\cos(\cos(x))$ is an even function, hence we know that: $$J_0(1)=\frac{2}{\pi}\int_0^{\pi/2} \cos(\cos(u))~du \iff \int_0^{\pi/2} \cos(\cos(u))~du=\frac{\pi J_0(1)}{2}$$

---

Evaluating $\lim\limits_{n\to \infty} I_n$:

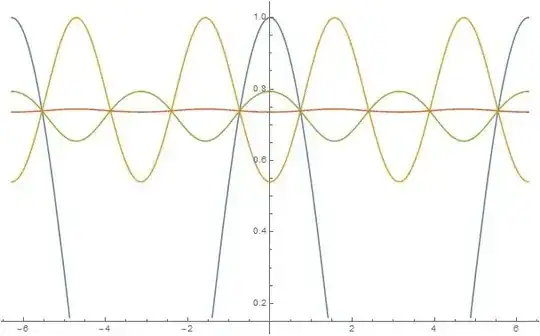
I realized that as $n\to \infty$, the integrand will converge to a constant function for all $x\in \mathbb{R}$, as shown below. The blue, yellow, green and red curves is when $n=1,2,5,10$ respectively.

I figured that we can represent the repeated composition of functions by the following recurrence $x_{n+1}=\cos(x_n)$. Using the principles of fixed point iteration, we know thus know that the value it tends to is the unique solution to $x=\cos(x)$. This turns out to be the Dottie Number, which I evaluated numerically using the Newton-Raphson Method and denoted this value by $\alpha$. I obtained: $$\alpha\approx 0.739085133215161$$ Hence: $$\lim_{n\to \infty} I_n=\int_0^{\pi/2}\cos(\cos(\cos(\dots(\cos(x))\dots)))~dx=\alpha\cdot \frac{\pi}{2} \approx 1.160952212443092$$

---

As mentioned, I am unsure how to evaluate closed forms for the cases when $n\geq 3$. I've checked some other definitions such as the Struve function $\mathbf{H}_{\gamma}(\cdot)$, though it only seems to be useful when evaluating $\int_0^{\pi/2} \sin(\sin(x))~dx$, which is not the integral we are considering. Hence, I would appreciate some guidance on how to evaluate a general closed form for $(1)$ for all $n\in \mathbb{N}$, if possible.

Answer 1

The mere fact that even the simple case $n=2$ ceases to possess a meaningful closed form in terms of elementary functions, and an entirely new function had to be invented from scratch in order to express its value, should be enough to settle all questions one might have concerning the possibility of finding such a form for larger values of the argument. Indeed, the very next case, $n=3,$ is not known to be expressible even in terms of special functions. That $\cos^{[\infty]}(x)$ is a constant $($since the function is both bound and monotone$)$ certainly constitutes a blessing, but such clearly does not hold for finite values of the iterator. $($ See also Liouville's theorem and the Risch algorithm $).$