In Stein's Complex Variables I'm having trouble verifying the conjecture in $(2.)$
$(1.)$
If $f$ is a complex-valued, on $\partial D$ and if it's absolute value $|f(z)|$ is bounded by a constant $M$ for all z on $\partial D$.
$$\left|\int_{\partial D} f(z)dz \right| \leq \max:=|f(z)|\int_{a}^{b} \gamma'(t)$$
$$\left|\int_{\partial D} f(z)\right | \leq \max_{z \, \in \, \partial D}\left|f(z) \right |\int_{a}^{b} \gamma'(t)$$
$$$$
$(2.)$
$$\int_{-\infty}^{\infty} \frac{e^{ix}-1}{x}dx = \frac{1}{2i}\int_{-\infty}^{\infty}\frac{e^{ix}-1}{x}dx = \frac{\pi}{2}$$
My initial task began within the given hint in $(1.)$, I focused on the integral on the RHS side, since it would be easier to define and transform the integral on our Semicircular Contour denoted by $\partial D$.
Lemma$(1.)$:
From $(2.)$ I observed that the integral now in $\mathbb{C}$ becomes the following:
$$\oint_{\partial D}\frac{e^{iz}-1}{z}dz$$
Remark: $\partial{D}$ denotes the boundary of our contour which can be depicted in the following image :
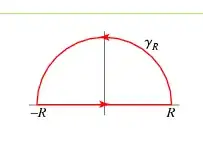
Lemma$(2)$
From Lemma(), our integral can be parametrized via the definition in $(1.3)$ as follows:
$$\frac{1}{2i}\oint_{\partial D}\frac{e^{rei\theta}-1}{re^{\theta}}iRe^{i\theta}d\theta, \, (0 \leq \theta \leq \pi)$$
$$\left|\frac{1}{2i}\oint_{\partial D} \frac{e^{ir^{ei\theta}}-1}{re^{i\theta}}\right | \leq \max_{z \, \in \, \partial D}\left|\frac{e^{ire^{i\theta}-1}}{re^{i\theta}} \right |\int_{a}^{b} \gamma'\left(\frac{e^{ire^{i\theta}-1}}{re^{i\theta}}\right)$$
One can construct the upper and lower bounds via the reverse triangle inequality as follows: $$|R(e^{ie\theta})-1|| \geq ||r(e^{ie\theta})-1|| ||R(e^{ie\theta})-1||$$ $$|R(e^{iei\theta})-1| \geq ||r(e^{(rei\theta)}-1|| R(e^{iei\theta})-1||$$
From this point in the problem i'm having troubles, on what's the next move to make would one take the $$\lim_{r \rightarrow \infty}\max_{\partial D}$$ and then calculate residues and apply the residue theorem ?