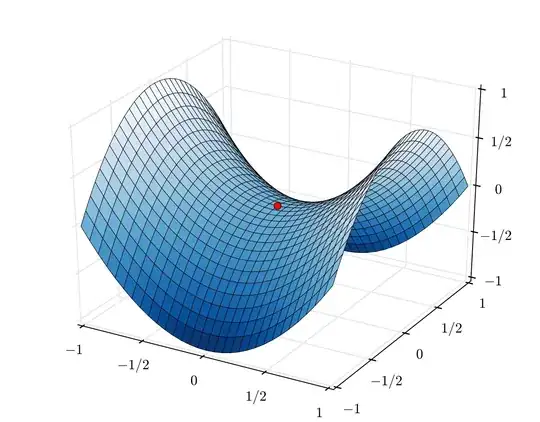
I have not yet had the privilege of studying multivariable calculus, but I have made an educated guess about how to find the minimum or maximum of a function with two variables, for example, $x$ and $y$.
Since, in three dimensions, a minimum or maximum would be represented by a tangent plane with no slope in any direction, could I treat $y$ as a constant and differentiate $z$ with respect to $x$, then treat $x$ as a constant and differentiate with respect to $y$, and find the places where both of these two are equal to zero?
Sorry if this is just a stupid assumption... it may be one of those things that just seems correct but is actually wrong.