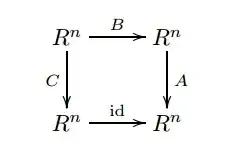
On a paper I'm reading, the author (Fulton) asks to apply the Snake Lemma to a square diagram:
how is that possible? I tried to construct a standard snake lemma diagram starting from this one, but didn't succeed. In this contest $R$ is a discrete valuation ring, and $A,B,C$ are matrices with entries in $R$ with determinant not $0$ which of course satisfy $C=AB$ (from the diagram).