The simplest $\Gamma_{\mathfrak B}$ graph where squares are separated by two hexagons...

Question

Let's call a bicubic planar graph build up of faces having degree $4$ and $6$ only, a $\Gamma_{\mathfrak B}$ graph. The simplest one is the truncated octahedron. Its planar drawing looks like the following:

Obviously every square is separated by at least one hexagon.

What is the simplest $\Gamma_{\mathfrak B}$ graph where the squares are separated by at least two hexagons?

I found a way to extend it by traversing it in the following way (the sharp turns of the outmost edge are due to Paint and not vertices of degree $2$):

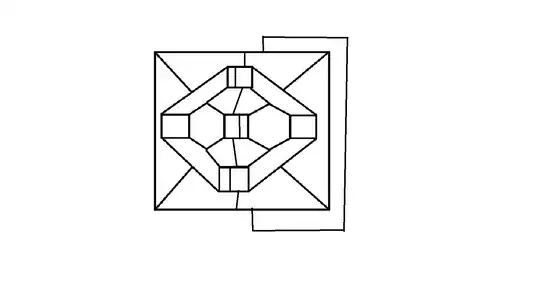
But it get's messy when I continue traversing, so I thought there is a way to simply expand a hexagon. Any idea welcome...

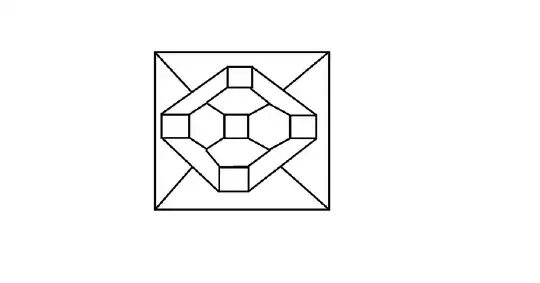
every square is separated by at least one hexagon. Please clarify what does it mean. — Smylic, May 22 '17 at 15:24
@Smylic going from one square to another, you have to go through at least one hexagon... — draks ..., May 23 '17 at 07:33
How do you draw the diagrams in your question ? (What software do you use ?) ... I would call them trivalent planar graphs ... why do you use the word bicubic ? — Donald Splutterwit, May 23 '17 at 15:12
@DonaldSplutterwit that's just windows Paint. Trivalent is just cubic and bicubic means bipartite and cubic... — draks ..., May 23 '17 at 21:31

score 2 · Accepted Answer · edited May 23 '17 at 06:58

2

The picture shows one example of 2 lines crossing the original graph and one round trip leaving all squares separated by at least 2 hexagons.

edited May 23 '17 at 06:58

draks ...

18,449

answered May 22 '17 at 23:33

E9BF

86

ugly, but correct... – draks ... May 23 '17 at 07:35

The simplest $\Gamma_{\mathfrak B}$ graph where squares are separated by two hexagons...

1 Answers1