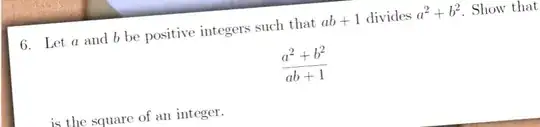let us suppose that there is given such kind of conjecture
if their division is square of integer then we will have
$\frac{a^2+b^2}{ab+1}=k^2$
for some integer $k$, then we would have
$a^2+b^2=k^2*ab+k^2$
or we would have
$a^2-k^2*a*b+b^2=k^2$
compare to the equation
$a^2-2*a*b+b^2=(a-b)^2$
we would have
$k^2=2$
but is that proof ? i could not understand if there is another option or alternative ways
If your reasoning was correct, then you would have proven that $\frac{a^2+b^2}{ab+1}$ is not the square of an integer, since you end up with $k^2 = 2$ for some integer $k$, which is a contradiction.
But, you make a mistake when you 'compare'
$a^2-k^2*a*b+b^2=k^2$
with
$a^2-2*a*b+b^2=(a-b)^2$
and conclude $k^2=2$ to make these equations match. But why should these equations have to match? Yes, if $k^2 = (a-b)^2$ then we can conclude $k^2 = 2$, but why should we believe that $k^2=(a-b)^2$? There is nothing in our givens that would say that ... all we know is that $k^2$ is some square. (in fact, we know it cannot be $(a-b)^2$, for then we obtain $k^2=2$, i.e. a contradiction!)
More importantly, though, what you have to prove is that $\frac{a^2+b^2}{ab+1}$ is always a square once we know that $ab+1|a^2+b^2$. So, assuming it is a square is assuming exactly what you need to prove, and is at best giving you confirmation that it could be a square, and at worst giving you some kind of circular argument.
