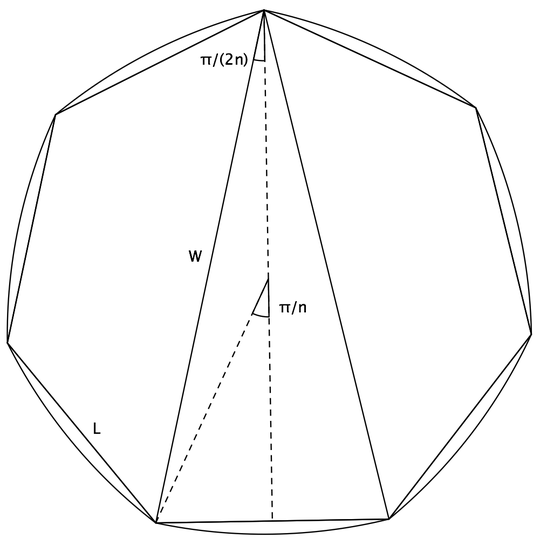
I derived a parametric formula for Reuleaux polygons some time ago in this blog entry.
To make this post self-contained, here are the equations:
$$\begin{align*}
x&=2\cos\frac{\pi}{2n}\cos\left(\frac12\left(t+\frac{\pi}{n}\left(2\left\lfloor\frac{n t}{2\pi}\right\rfloor+1\right)\right)\right)-\cos\left(\frac{\pi}{n}\left(2\left\lfloor\frac{n t}{2\pi}\right\rfloor+1\right)\right)\\
y&=2\cos\frac{\pi}{2n}\sin\left(\frac12\left(t+\frac{\pi}{n}\left(2\left\lfloor\frac{n t}{2\pi}\right\rfloor+1\right)\right)\right)-\sin\left(\frac{\pi}{n}\left(2\left\lfloor\frac{n t}{2\pi}\right\rfloor+1\right)\right)
\end{align*}$$
Here is a Mathematica demonstration:
Table[ParametricPlot[2 Cos[π/(2 n)] Exp[I (t + π (2 Floor[n t/(2 π)] + 1)/n)/2] -
Exp[I π (2 Floor[n t/(2 π)] + 1)/n] // ReIm, {t, 0, 2 π}],
{n, 3, 7, 2}] // GraphicsRow
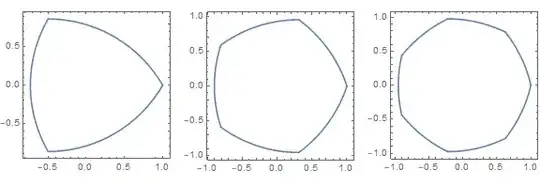
(Note the use of the complex form of the parametric equations.)
For some applications, a polar equation (like the one in this answer) might be more convenient. One can use the usual distance formula in polar coordinates to derive the polar equation of an $n$-sided Reuleaux polygon:
$$r=\cos\left(\theta -\frac{2\pi}{n}\left\lfloor\frac{n (\theta -\pi )}{2 \pi }+\frac{1}{2}\right\rfloor\right)+\sqrt{1+2\cos\frac{\pi}{n}+\cos^2\left(\theta -\frac{2\pi}{n}\left\lfloor\frac{n (\theta -\pi)}{2 \pi}+\frac{1}{2}\right\rfloor\right)}$$
In Mathematica, one can do this:
Table[PolarPlot[With[{c = Cos[θ - 2 π Floor[n (θ - π)/(2 π) + 1/2]/n]},
c + Sqrt[1 + 2 Cos[π/n] + c^2]], {θ, 0, 2 π}],
{n, 3, 7, 2}] // GraphicsRow
to get a picture identical to the one above.